【题目】如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
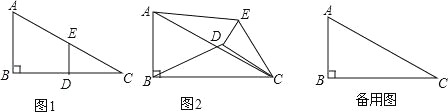
(1)问题发现
①当α=0°时,![]() = ;②当α=180°时,
= ;②当α=180°时,![]() = .
= .
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.
参考答案:
【答案】(1) ![]() ;
;![]() ;(2)没有变化;(3)
;(2)没有变化;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)①当α=0°时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出![]() 的值是多少.
的值是多少.
②α=180°时,可得AB∥DE,然后根据![]() ,求出
,求出![]() 的值是多少即可.
的值是多少即可.
(2)首先判断出∠ECA=∠DCB,再根据![]() ,判断出△ECA∽△DCB,即可求出
,判断出△ECA∽△DCB,即可求出![]() 的值是多少,进而判断出
的值是多少,进而判断出![]() 的大小没有变化即可.
的大小没有变化即可.
(3)根据题意,分两种情况:①点A,D,E所在的直线和BC平行时;②点A,D,E所在的直线和BC相交时;然后分类讨论,求出线段BD的长各是多少即可.
试题解析:(1)①当α=0°时,
∵Rt△ABC中,∠B=90°,
∴AC=![]() ,
,
∵点D、E分别是边BC、AC的中点,
∴![]() ,BD=8÷2=4,
,BD=8÷2=4,
∴![]() .
.
②如图1,
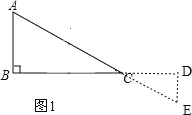 ,
,
当α=180°时,
可得AB∥DE,
∵![]() ,
,
∴![]()
(2)如图2,
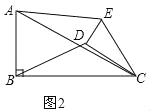 ,
,
当0°≤α<360°时,![]() 的大小没有变化,
的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵![]() ,
,
∴△ECA∽△DCB,
∴![]() .
.
(3)①如图3,
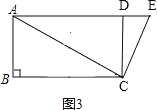 ,
,
∵AC=4![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD=![]()
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC=![]() .
.
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
 ,
,
∵AC=![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD=![]() ,
,
∵点D、E分别是边BC、AC的中点,
∴DE=![]() =2,
=2,
∴AE=AD-DE=8-2=6,
由(2),可得
![]() ,
,
∴BD=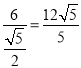 .
.
综上所述,BD的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线
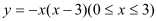 ,记为C1,它与
,记为C1,它与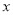 轴交于点O,A1;将C1绕点A1旋转180°得C2,交
轴交于点O,A1;将C1绕点A1旋转180°得C2,交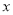 轴于点A2;将C2绕点A2旋转180°得C3,交
轴于点A2;将C2绕点A2旋转180°得C3,交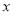 轴于点A3;……如此进行下去,得到一“波浪线”.若点P(41,
轴于点A3;……如此进行下去,得到一“波浪线”.若点P(41,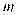 )在此“波浪线”上,则
)在此“波浪线”上,则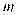 的值为
的值为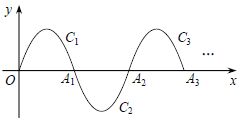
A.2 B.
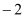 C.0 D.
C.0 D.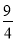
-
科目: 来源: 题型:
查看答案和解析>>【题目】把“同角的补角相等”写成“如果……那么……”的形式为____________________________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式x﹣1≤10的解集是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当两条不同的直线有一个公共点时,我们就称这两条直线___________,这个公共点叫做它们的___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励创业,市政府制定了小型企业的优惠政策,许多小型企业应运而生,我县统计了2015年1-5月新注册小型企业的数量,并将结果绘制成如图所示两种不完整的统计图:

(1)我县2015年1-5月新注册小型企业一共有 家.扇形统计图中“2月”所在扇形的圆心角为 度;
(2) 请将折线统计图补充完整;
(3)在2015年3月新注册的小型企业中,只有2家是餐饮企业,现从3月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形中30°角所对的直角边为2cm,则斜边的长为( )
A.2cm
B.4cm
C.6cm
D.8cm
相关试题

