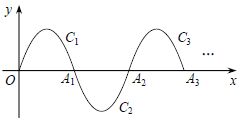
【题目】如图,一段抛物线![]() ,记为C1,它与
,记为C1,它与![]() 轴交于点O,A1;将C1绕点A1旋转180°得C2,交
轴交于点O,A1;将C1绕点A1旋转180°得C2,交![]() 轴于点A2;将C2绕点A2旋转180°得C3,交
轴于点A2;将C2绕点A2旋转180°得C3,交![]() 轴于点A3;……如此进行下去,得到一“波浪线”.若点P(41,
轴于点A3;……如此进行下去,得到一“波浪线”.若点P(41,![]() )在此“波浪线”上,则
)在此“波浪线”上,则![]() 的值为
的值为
A.2 B.![]() C.0 D.
C.0 D.![]()
参考答案:
【答案】B.
【解析】
试题解析:当y=0时,-x(x-3)=0,解得x1=0,x2=3,则A1(3,0),OA1=3,
∵C1绕A1旋转180°得到C2,
∴A1A2=OA1=3,则OA2=6,A2(6,0),
∴C2的解析式为y=(x-3)(x-6)(3≤x≤6),
同样可得OA13=39,OA14=42,则A13(39,0),A14(42,0),
∴C14的解析式为y=(x-39)(x-42)(39≤x≤42),
∴点P(41,m)在抛物线C14上,
当x=41时,m=2×(-1)=-2.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是
A. 经过两点有且只有一条线段 B. 经过两点有且只有一条直线
C. 经过两点有且只有一条射线 D. 经过两点有无数条直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=x2﹣2x+3沿x轴向右平移2个单位,得到的抛物线解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a2+3a2=4a4 B. 3a2a=3a3 C. (3a3)2=9a5 D. (2a+1)2=4a2+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】把“同角的补角相等”写成“如果……那么……”的形式为____________________________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式x﹣1≤10的解集是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
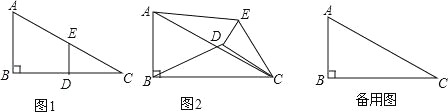
(1)问题发现
①当α=0°时,
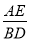 = ;②当α=180°时,
= ;②当α=180°时,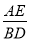 = .
= .(2)拓展探究
试判断:当0°≤α<360°时,
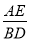 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.(3)问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.
相关试题

