【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?

参考答案:
【答案】(1)y=﹣0.1x+8(30≤x≤60)(2)w= (3)当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元
(3)当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元
【解析】试题分析:(1)由图象知,当30≤x≤60时,图象过(60,2)和(30,5),运用待定系数法求解析式即可;
(2)根据销售产品的纯利润=销售量×单个利润,分30≤x≤60和60<x≤80列函数表达式;
(3)当30≤x≤60时,运用二次函数性质解决,当60<x≤80时,运用反比例函数性质解答.
试题解析:(1)当x=60时,y=![]() =2,
=2,
∴当30≤x≤60时,图象过(60,2)和(30,5),
设y=kx+b,则![]() ,
,
解得: ![]() ,
,
∴y=﹣0.1x+8(30≤x≤60);
(2)根据题意,当30≤x≤60时,W=(x﹣20)y﹣50=(x﹣20)(﹣0.1x+8)﹣50=![]() +10x﹣210,
+10x﹣210,
当60<x≤80时,W=(x﹣20)y﹣50=(x﹣20)![]() ﹣50=
﹣50=![]() +70,
+70,
综上所述:W= ;
;
(3)当30≤x≤60时,W=![]() +10x﹣210=
+10x﹣210=![]() ,
,
当x=50时, ![]() =40(万元);
=40(万元);
当60<x≤80时,W=![]() +70,
+70,
∵﹣2400<0,W随x的增大而增大,
∴当x=80时, ![]() =
=![]() +70=40(万元),
+70=40(万元),
答:当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N. 给出下列结论:①△ABM≌△CDN;②AM=
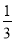 AC;③DN=2NF;④S△AMB=
AC;③DN=2NF;④S△AMB=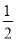 S△ABC.其中正确的结论是_______________(只填番号)
S△ABC.其中正确的结论是_______________(只填番号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F.
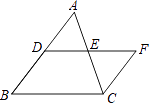
(1)求证:DE=EF.
(2)分别连结DC、AF,若AC=BC,试判断四边形ADCF的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(-2a2b) 2+a32ab 2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A 非常赞同;B 赞同但要有时间限制;C 无所谓;D 不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的外接圆⊙O,那么点O是△ABC的( )
A.三条中线交点B.三条高的交点
C.三条边的垂直平分线的交点D.三条角平分线交点
-
科目: 来源: 题型:
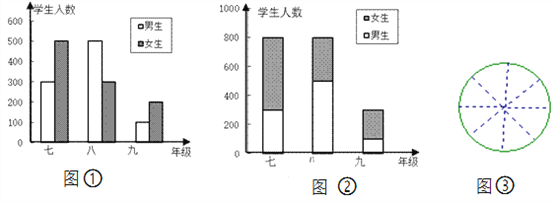
查看答案和解析>>【题目】图①、图②是李晓同学根据所在学校三个年级男女生人数画出的两幅条形图.
(1)两个图中哪个能更好地反映学校每个年级学生的总人数?哪个图能更好地比较每个年级男女生的人数?
(2)请按该校各年级学生人数在图③中画出扇形统计图.
相关试题

