【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一动点,
上一动点,![]() 且
且![]() ,连接
,连接![]() ,其中
,其中![]() .
.
问题发现:(1)如图1,若![]() ,
,![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?![]() 的值为多少?直接写出答案;
的值为多少?直接写出答案;
类比探究,(2)如图2,若![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?![]() 的值为多少?请说明理由.
的值为多少?请说明理由.
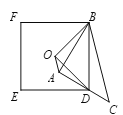
拓展应用:(3)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,以
上一点,以![]() 为边,在如图所示位置作正方形
为边,在如图所示位置作正方形![]() ,点
,点![]() 为正方形
为正方形![]() 的对称中心,且
的对称中心,且![]() ,请直接写出
,请直接写出![]() 的长.
的长.

参考答案:
【答案】(1)∠BCE=∠A=60°;k=1;(2)∠BCE=∠A,k=![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)证明![]() ,得
,得![]() ,
,![]() 即可得解;
即可得解;
(2)先证明△ABC∽△DBE,![]() ,结合∠ABD=∠CBE,根据对应边成比例且夹角相等可证明△ABD∽△CBE,即可得出结论;
,结合∠ABD=∠CBE,根据对应边成比例且夹角相等可证明△ABD∽△CBE,即可得出结论;
(3)连接BO、OD,通过证明![]() ∽
∽![]() ,再根据相似三角形对应边成比例,求出DC,进而求出AD,再利用勾股定理求DB,则DE=DB.
,再根据相似三角形对应边成比例,求出DC,进而求出AD,再利用勾股定理求DB,则DE=DB.
解:(1)∵![]() ,
, ![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
又∵![]() 且
且![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
故答案为:![]() ,
,![]() .
.
(2)∠BCE=∠A,k=![]() .
.
理由如下:∵∠BAC=∠BDE,AB=AC,BD=DE,
∴∠ABC=∠DBE,
∴△ABC∽△DBE,
∴![]() ,
,
又∵∠ABC+∠CBD=∠DBE+∠CBD,即∠ABD=∠CBE
∴△ABD∽△CBE(对应边成比例,夹角相等),
∴![]() ,
,![]() ;
;
(3)如图,连接BO、OD,
∵四边形![]() 为正方形,点
为正方形,点![]() 为正方形
为正方形![]() 的对称中心,
的对称中心,
∴![]() ,
,![]() ,
,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() 的长为:
的长为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活质量的提高,越来越多的人们关注运动与健康,近来“微信运动”逐渐被大家关注和喜爱.某兴趣小组为了了解某社区居民的“微信运动”情况,进行了随机抽样调查,对他们一日“微信运动”中的步数进行了统计,下面给出部分信息:
①
 (步数/日)
(步数/日)频数
频率
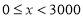
5
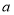
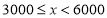
10
0.2

15
0.3
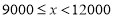
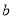
0.2
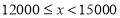
8
0.16
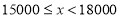
2
0.04
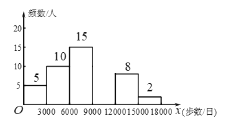
 这一组的数据为:
这一组的数据为:6000 6200 6200 6500 6600 6800 7000 7200 7200 7200 7800 8000 8300 8700 8900
根据以上信息,回答下列问题:
(1)本次被调查的居民有__________人:表中
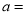 ______________,
______________,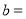 ___________;
___________;(2)补全频数分布直方图;
(3)直接写出被调查的居民在“微信运动”中步数的中位数;
(4)本社区约有5000人,用调查样本估计一日步数不低于9000步的人数.
-
科目: 来源: 题型:
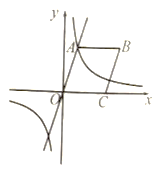
查看答案和解析>>【题目】如图,已知正比例函数
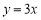 与反比例函数
与反比例函数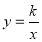 的图象相交于点
的图象相交于点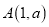 .
.
(1)填空:
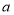 的值为_______________,
的值为_______________,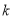 的值为_____________;
的值为_____________;(2)以点
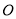 为圆心、
为圆心、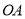 为半径画弧交
为半径画弧交 轴的正半轴于点
轴的正半轴于点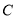 ,以
,以 为邻边作平行四边形
为邻边作平行四边形 ,求点
,求点 的坐标;
的坐标;(3)观察上述反比例函数
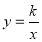 的图象,当
的图象,当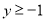 时,请直接写出自变量
时,请直接写出自变量 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店经销进价分别为
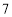 元/千克、
元/千克、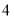 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)时间
甲水果销量
乙水果销量
销售收入
周五
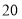 千克
千克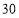 千克
千克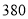 元
元周六
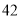 千克
千克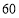 千克
千克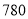 元
元(1)求甲、乙两种水果的销售单价;
(2)若水果店准备用不多于
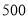 元的资金再购进两种水果共
元的资金再购进两种水果共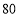 千克,求最多能够进甲水果多少千克?
千克,求最多能够进甲水果多少千克?(3)在(2)的条件下,水果店销售完这
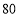 千克水果能否实现利润为
千克水果能否实现利润为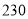 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
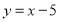 分别与
分别与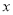 轴、
轴、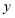 轴交于点
轴交于点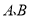 ,抛物线
,抛物线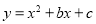 经过点
经过点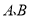 ,与
,与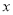 轴的另一个交点为
轴的另一个交点为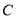 ,抛物线的对称轴
,抛物线的对称轴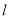 交
交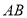 于点
于点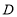 .
.(1)求抛物线的函数关系式及对称轴;
(2)若
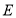 为
为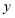 轴上一动点,
轴上一动点,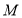 为
为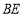 的中点,过点
的中点,过点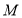 作
作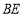 的中垂线,交抛物线于点
的中垂线,交抛物线于点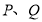 ,其中
,其中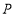 在
在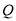 的左边.
的左边.①如图1,若
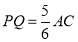 时,求
时,求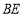 的长.
的长.②当以点
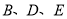 为顶点的三角形是直角三角形时,请直接写出点
为顶点的三角形是直角三角形时,请直接写出点 的坐标.
的坐标.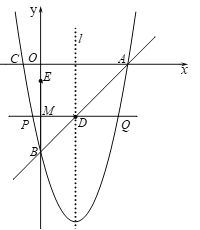

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级( 3 )班全体学生 2019 年初中毕业体育考试的成绩统计如下表:
成绩
35
39
42
43
45
49
50
人数
3
5
6
6
8
7
5
根据上表中的信息判断,下列结论中错误的是 ( )
A.该班一共有 40 名同学B.该班学生这次考试成绩的众数是 45 分
C.该班学生这次考试成绩的中位数是 44 分D.该班学生这次考试成绩的平均数是 45 分
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市举行职工五人制足球联赛,共赛 17 轮(即每队均需参赛 17 场),记分办法是胜一场得 3分,平一场得 1 分,负一场得 0 分 . 若
 足球队总积分为 16 分,且踢平场数是所负场数的整数倍,试推算
足球队总积分为 16 分,且踢平场数是所负场数的整数倍,试推算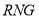 足球队所负场数的情况有( )
足球队所负场数的情况有( )A.1 种B.2 种C.3 种D.4 种
相关试题

