【题目】某水果店经销进价分别为![]() 元/千克、
元/千克、![]() 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
时间 | 甲水果销量 | 乙水果销量 | 销售收入 |
周五 |
|
|
|
周六 |
|
|
|
(1)求甲、乙两种水果的销售单价;
(2)若水果店准备用不多于![]() 元的资金再购进两种水果共
元的资金再购进两种水果共![]() 千克,求最多能够进甲水果多少千克?
千克,求最多能够进甲水果多少千克?
(3)在(2)的条件下,水果店销售完这![]() 千克水果能否实现利润为
千克水果能否实现利润为![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
参考答案:
【答案】(1)甲、乙两种水果的销售单价分别为![]() 元、
元、![]() 元;(2)最多购进甲水果
元;(2)最多购进甲水果![]() 千克时,采购资金不多于
千克时,采购资金不多于![]() 元;(3)在(2)的条件下水果店不能实现利润
元;(3)在(2)的条件下水果店不能实现利润![]() 元的目标.
元的目标.
【解析】
(1)设甲、乙两种水果的销售单价分别为![]() 元、
元、![]() 元,根据题意找到等量关系进行列二元一次方程组进行求解;
元,根据题意找到等量关系进行列二元一次方程组进行求解;
(2)设购进甲水果为![]() 千克,乙水果
千克,乙水果![]() 千克时采购资金不多于
千克时采购资金不多于![]() 元,根据题意列出不等式即可求解;
元,根据题意列出不等式即可求解;
(3)根据题意找到等量关系列出方程即可求解.
解:(1)设甲、乙两种水果的销售单价分别为![]() 元、
元、![]() 元,依题意得:
元,依题意得:
![]() 解得:
解得:![]()
所以甲、乙两种水果的销售单价分别为![]() 元、
元、![]() 元
元
(2)设购进甲水果为![]() 千克,乙水果
千克,乙水果![]() 千克时采购资金不多于
千克时采购资金不多于![]() 元;
元;
根据题意得:![]() .
.
解得:![]()
所以最多购进甲水果![]() 千克时,采购资金不多于
千克时,采购资金不多于![]() 元
元
(3)依题意得:
![]()
解得:![]()
因为![]() ,
,
所以在(2)的条件下水果店不能实现利润![]() 元的目标.
元的目标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的
 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
-
科目: 来源: 题型:
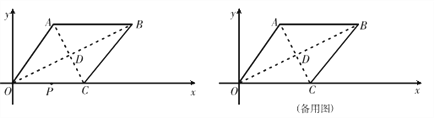
查看答案和解析>>【题目】如图,在菱形 OA BC 中,已知点 B(8,4),C(5,0),
点 D 为 OB、AC 交点,点 P 从原点出发向 x 轴正方向运动;
(1) 在点 P 运动过程中,若∠OBP=900,求出点 P 坐标;
(2) 在点 P 运动过程中,若∠PDC+∠BCP=900,求出点 P 坐标;
(3) 点 P 在(2)的位置时停止运动,点 M 从点 P 出发沿 x 轴正方向运动,连结 BM,若点 P 关于BM 的对称点 P’到 AB 所在直线的距离为 2,求此时点 M 的坐标.
-
科目: 来源: 题型:
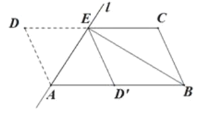
查看答案和解析>>【题目】如图,将
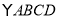 沿过点
沿过点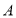 的直线
的直线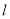 折叠,使点
折叠,使点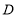 落到
落到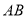 边上的
边上的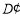 处,折痕交
处,折痕交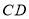 边于点
边于点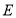 ,连接
,连接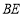 .
.
(1)求证:四边形
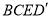 是平行四边形;
是平行四边形;(2)若
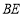 平分
平分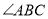 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
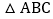 中,
中,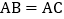 ,D在边AC上,且
,D在边AC上,且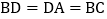 .
.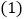 如图1,填空
如图1,填空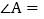 ______
______ ,
,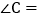 ______
______
 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线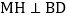 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E. 求证:
求证: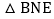 是等腰三角形;
是等腰三角形; 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.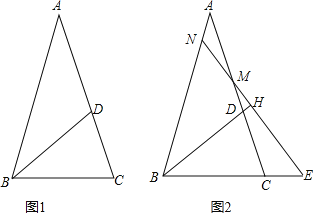
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,在平面直角坐标系中 ,已知二次函数y=ax2+bx+c (a≠0)
的图象经过 A(-1,0),B(3,0),C(6,4)三点.
(1)求此二次函数解析式和顶点 D 的坐标;
(2)①E为抛物线对称轴上一点,过点E作FG//x 轴,分别交抛物线于F、G两点 ,若
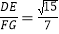 ,求点E的坐标;
,求点E的坐标;② 若抛物线对称轴上点 H 到直线 BC 的距离等于点 H 到 x 轴的距离,则求出点 H
的坐标;
(3)在(2)的条件下,以点I(1,
 )为圆心,IH 的长为半径作⊙I,J 为⊙I上的动点,求是否存在一个定值
)为圆心,IH 的长为半径作⊙I,J 为⊙I上的动点,求是否存在一个定值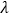 ,使得 CJ+
,使得 CJ+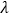 EJ 的最小值是
EJ 的最小值是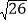 若不存在,请说明理由.若存在,请求出
若不存在,请说明理由.若存在,请求出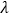 的值;
的值;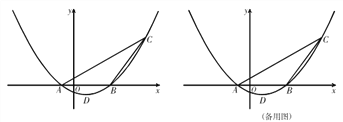
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D,E分别在AC,AB上,且AD=AE,点O是BD和CE的交点,则:①△ABD≌△ACE;②△BOE≌△COD;③点O在∠BAC的平分线上,以上结论( )
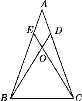
A.都正确B.都不正确
C.只有一个正确D.只有一个不正确
相关试题

