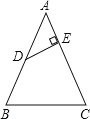
【题目】如图,在△ABC中,AB=AC=26cm,BC=20cm,D是AB的中点,过D作DE⊥AC于E,则DE的长为____.
参考答案:
【答案】![]() cm.
cm.
【解析】
过A作BC的垂线,由勾股定理易求得此垂线的长,即可求出△ABC的面积;连接CD,由于AD=BD,则△ADC、△BCD等底同高,它们的面积相等,由此可得到△ACD的面积;进而可根据△ACD的面积求出DE的长.
解:过A作AF⊥BC于F,连接CD;
△ABC中,AB=AC=26cm,AF⊥BC,则BF=FC![]() BC=10(cm);
BC=10(cm);
Rt△ABF中,AB=26cm,BF=10cm;
由勾股定理,得AF![]() 24(cm);
24(cm);
∴S△ABC![]() BCAF=240(cm2).
BCAF=240(cm2).
∵AD=BD,
∴S△ADC=S△BCD![]() S△ABC=120(cm2).
S△ABC=120(cm2).
∵S△ADC![]() ACDE=120(cm2),
ACDE=120(cm2),
则DE![]() (cm).
(cm).
故答案为:![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】河大附中初一年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CA=CB,M,N分别AB上的两动点,且∠MCN=45°,下列结论:①
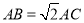 ;②CM2﹣CN2=NBNA﹣MBMA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
;②CM2﹣CN2=NBNA﹣MBMA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,高AD=12,则
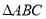 的周长为_______________.
的周长为_______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)若由甲挑一名选手打第一场比赛,选中乙的概率是多少?(直接写出答案)
(2)任选两名同学打第一场,请用树状图或列表法求恰好选中甲、乙两位同学的概率。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 、
、  是关于
是关于  的方程
的方程  的两个不相等的实数根.
的两个不相等的实数根.
(1)求实数 的取值范围;
的取值范围;
(2)已知等腰 的一边长为7,若
的一边长为7,若  、
、  恰好是
恰好是  另外两边长,求这个三角形的周长.
另外两边长,求这个三角形的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坐标系中放一矩形OABC,AB=2,OA=1,现将矩形OABC沿x轴的正方向无滑动翻转,每次翻转90°,连续翻转2019次,点B的落点依次为B1,B2,B3,B4…,则B2019的坐标为____.

相关试题

