【题目】河大附中初一年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
参考答案:
【答案】(1)A、B型车每辆可分别载学生30人,40人;(2)租用1辆A型8辆B型车花费最少为1060元.
【解析】
(1)根据载客量,可得方程组,根据解方程组,可得答案;
(2)根据题意列出方程,可得答案.
(1)设A、B型车每辆可分别载学生x,y人,
可得:![]() ,
,
解得:![]() ,
,
答:A、B型车每辆可分别载学生30人,40人;
(2)设租用A型a辆,B型b辆,
可得:30a+40b=350,
因为a,b为正整数,所以方程的解为:![]() ,
,![]() ,
,![]() ,
,
方案一:A型1辆,B型8辆,费用:100×1+120×8=1060元;
方案二:A型5辆,B型5辆,费用:100×5+120×5=1100元;
方案三:A型9辆,B型2辆,费用:100×9+120×2=1140元;
所以租用1辆A型8辆B型车花费最少为1060元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
(1)完成表中填空①;②;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为 ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
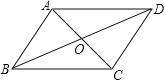
A.AB=DC,AD=BCB.AB∥DC,AD∥BC
C.AB∥DC,AD=BCD.OA=OC,OB=OD
-
科目: 来源: 题型:
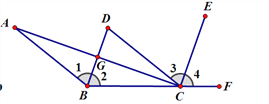
查看答案和解析>>【题目】如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CA=CB,M,N分别AB上的两动点,且∠MCN=45°,下列结论:①
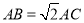 ;②CM2﹣CN2=NBNA﹣MBMA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
;②CM2﹣CN2=NBNA﹣MBMA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )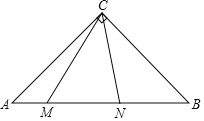
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,高AD=12,则
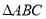 的周长为_______________.
的周长为_______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=26cm,BC=20cm,D是AB的中点,过D作DE⊥AC于E,则DE的长为____.
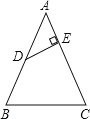
相关试题

