【题目】已知 ![]() 、
、 ![]() 是关于
是关于 ![]() 的方程
的方程 ![]() 的两个不相等的实数根.
的两个不相等的实数根.
(1)求实数 ![]() 的取值范围;
的取值范围;
(2)已知等腰 ![]() 的一边长为7,若
的一边长为7,若 ![]() 、
、 ![]() 恰好是
恰好是 ![]() 另外两边长,求这个三角形的周长.
另外两边长,求这个三角形的周长.
参考答案:
【答案】
(1)解:由题意得△=4(m+1)2﹣4(m2+5)=8m-16>0,解得:m>2;
(2)解:由题意,∵x1≠x2时,∴只能取x1=7或x2=7,即7是方程的一个根,将x=7代入得:49﹣14(m+1)+m2+5=0,解得:m=4或m=10.
当m=4时,方程的另一个根为3,此时三角形三边分别为7、7、3,周长为17;
当m=10时,方程的另一个根为15,此时不能构成三角形;
故三角形的周长为17.
【解析】(1)二次项系数不含字母,由判别式△>0,可求出m范围;(2)需分类讨论,由等腰三角形的性质可得出7是方程的一个根,代入方程,求出m的值,再验证是否构成三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,高AD=12,则
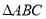 的周长为_______________.
的周长为_______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=26cm,BC=20cm,D是AB的中点,过D作DE⊥AC于E,则DE的长为____.
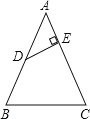
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)若由甲挑一名选手打第一场比赛,选中乙的概率是多少?(直接写出答案)
(2)任选两名同学打第一场,请用树状图或列表法求恰好选中甲、乙两位同学的概率。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坐标系中放一矩形OABC,AB=2,OA=1,现将矩形OABC沿x轴的正方向无滑动翻转,每次翻转90°,连续翻转2019次,点B的落点依次为B1,B2,B3,B4…,则B2019的坐标为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
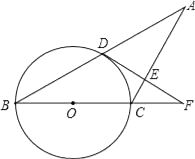
求证:
(1)AD=BD;
(2)DF是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
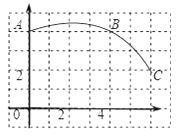
(1)请在图中确定该圆弧所在圆心D点的位置,求出D点坐标
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
相关试题

