【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.

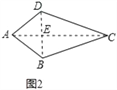
(l)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探宄:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证)
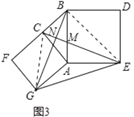
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.

参考答案:
【答案】(1)四边形ABCD是垂美四边形,理由见解析;(2)猜想结论:垂美四边形的两组对边的平方和相等,过程见解析;(3)GE=![]()
【解析】试题分析:(1)根据垂直平分线的判定定理可得,直线AC是线段BD的垂直平分线,结论得证;
(2)根据垂直的定义可得∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得AD2+BC2=AE2+DE2+BE2+CE2,进而得到答案;
(3)连接CG、BE,由题意易得△GAB≌△CAE,可知∠ABG=∠AEC,进而得到四边形BCGE是垂美四边形;接下来根据垂美四边形的性质、勾股定理以及(2)的结论进行计算求解,即可完成解答.
试题解析:
解:(1)四边形ABCD是垂美四边形.
证明:∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)猜想结论:垂美四边形的两组对边的平方和相等.
如图2,已知四边形ABCD中,AC⊥BD,垂足为E,
求证:AD2+BC2=AB2+CD2
证明:∵AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,
AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2;
(3)连接CG、BE,
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,
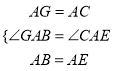 ,
,
∴△GAB≌△CAE,
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=3,CG=4![]() ,BE=5
,BE=5![]() ,
,
∴GE2=CG2+BE2﹣CB2=73,
∴GE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并解决问题.
材料:一般地,
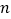 个相同的因数
个相同的因数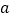 相乘,记为
相乘,记为 .如
.如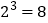 ,此时,
,此时, 叫做以
叫做以 为底
为底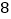 的对数,记为
的对数,记为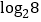 (即
(即 ).一般地,若
).一般地,若 (
( 且
且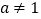 ,
, ),则
),则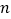 叫做以
叫做以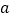 为底
为底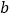 的对数,记为
的对数,记为 (即
(即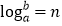 ).如
).如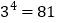 ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为 (即
(即 ).
).问题:
(1)计算以下各式的值:
 ;
; 。
。(2)写出
 ,
,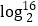 ,
,  之间满足的等量关系。
之间满足的等量关系。(3)由(2)的结果,将归纳出的一般性结论填写在横线上。
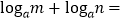 。(a>0且a≠1,m>0,n>0)
。(a>0且a≠1,m>0,n>0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,E是对角线AC上一点.
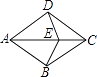
(1)求证:△ABE≌△ADE;
(2)若AB=AE,∠BAE=36°,求∠CDE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】李先生上星期日买进某公司股票2000股,每股20元,下表为本周内每日该股票的涨跌情况.(单位:元)
星期
一
二
三
四
五
六
每股涨跌
+4
+4.5
-1
-2.5
-6

(1)本周内最低价每股多少元?
(2)已知李先生买进股票时付了
 的手续费,卖出时需付成交额
的手续费,卖出时需付成交额 的手续费和
的手续费和 的交易税,如果李先生在星期三收盘前将全部股票卖出,他的收益情况如何?
的交易税,如果李先生在星期三收盘前将全部股票卖出,他的收益情况如何? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是某班学生上学的三种方式(乘车、步行、骑车)的人数分布直方图和扇形图2.
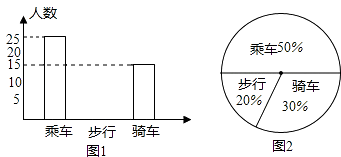
(1)该班有多少名学生;
(2)补上人数分布直方图的空缺部分;
(3)若全年级有800人,估计该年级步行有名学生. -
科目: 来源: 题型:
查看答案和解析>>【题目】请观察下列算式,找出规律并填空。
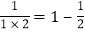 ,
,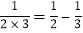 ,
,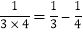 ,
,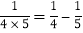 ···
···根据以上规律解答以下三题:
(1) 第10个等式是:__________=_____________
第n个等式是:__________=_____________
(2)计算:
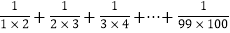 的值。
的值。(3)若有理数
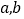 满足
满足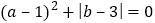 ,试求:
,试求: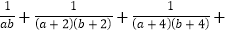
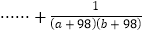 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】“红树林小组”全体组员参加了义务植树活动,领得准备种植的树苗一批,组长决定采用分工负责制,经计算发现:若每位组员种植10棵树苗,则还剩88棵;若每位组员种植12棵树苗,则有一位组员种植的树苗不到4棵,求准备种植树苗的棵数和“红树林小组”的人数.
相关试题

