【题目】为节约能源,优化电力资源配置,提高电力供应的整体效益,国家实行了错峰用电.某地区的居民用电,按白天时段和晚间时段规定了不同的单价.某户5月份白天时段用电量比晚间时段用电量多![]() ,6月份白天时段用电量比5月份白天时段用电量少
,6月份白天时段用电量比5月份白天时段用电量少![]() ,结果6月份的总用电量比5月份的总用电量多
,结果6月份的总用电量比5月份的总用电量多![]() ,但6月份的电费却比5月份的电费少
,但6月份的电费却比5月份的电费少![]() ,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】A
【解析】
设该地区白天时段居民用电的单价为a,晚间用电的单价为b,该户5月份晚间时段用电量为x,先根据题意分别求出5月份白天时段用电量、6月份白天时段和晚间时段用电量,再根据“6月份的电费却比5月份的电费少![]() ”列出方程,求出a、b的关系,从而可得出答案.
”列出方程,求出a、b的关系,从而可得出答案.
设该地区白天时段居民用电的单价为a,晚间用电的单价为b,该户5月份晚间时段用电量为x,则5月份白天时段用电量为![]() ,5月份的总用电量为
,5月份的总用电量为![]()
由题意得:该户6月份白天时段用电量为![]() ,6月份的总用电量为
,6月份的总用电量为![]() ,则6月份晚间时段用电量为
,则6月份晚间时段用电量为![]()
因此,该户5月份的电费为![]() ;6月份的电费为
;6月份的电费为![]()
则有:![]()
解得:![]() ,即
,即![]()
则 ,即晚间用电的单价比白天用电的单价低
,即晚间用电的单价比白天用电的单价低![]()
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一副三角板,如图放置在桌面上,让三角板OAB的30°角顶点与三角板OCD的直角顶点重合,边OA与OC重合,固定三角板OCD不动,把三角板OAB绕着顶点O顺时针转动,直到边OB落在桌面上为止.

(1)如下图,当三角板OAB转动了20°时,求∠BOD的度数;
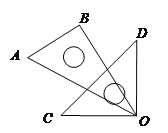
(2)在转动过程中,若∠BOD=20°,在下面两图中分别画出∠AOB的位置,并求出转动了多少度?
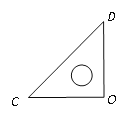

(3)在转动过程中,∠AOC与∠BOD有怎样的等量关系,请你给出相等关系式,并说明理由;


-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 上部分点的横坐标
上部分点的横坐标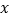 ,纵坐标
,纵坐标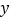 的对应值如下表:
的对应值如下表:x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数
 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是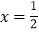 ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )A. ①② B. ①③ C. ①②③ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2
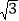 ,则∠A的度数为____________ .
,则∠A的度数为____________ .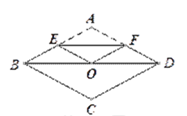
-
科目: 来源: 题型:
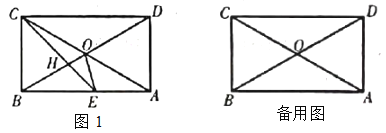
查看答案和解析>>【题目】如图,矩形
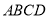 中,
中,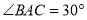 ,对角线
,对角线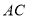 、
、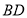 交于点
交于点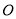 ,
,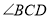 的平分线
的平分线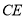 分别交
分别交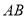 、
、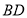 于点
于点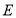 、
、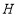 ,连接
,连接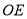 .
.
(l)求
 的度数;
的度数;(2)若
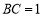 ,求
,求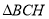 的面积;
的面积;(3)求
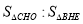 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平面直角坐标系中,
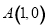 、
、 ,现将线段
,现将线段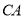 绕
绕 点顺时针旋转
点顺时针旋转 得到点
得到点 ,连接
,连接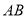 .
.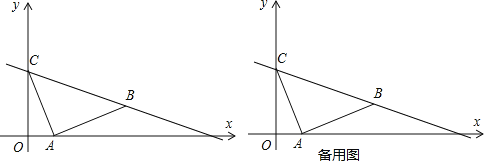
(1)求出直线
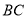 的解析式;
的解析式;(2)若动点
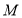 从点
从点 出发,沿线段
出发,沿线段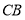 以每分钟
以每分钟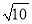 个单位的速度运动,过
个单位的速度运动,过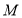 作
作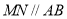 交
交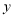 轴于
轴于 ,连接
,连接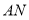 .设运动时间为
.设运动时间为 分钟,当四边形
分钟,当四边形 为平行四边形时,求
为平行四边形时,求 的值.
的值.(3)
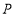 为直线
为直线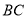 上一点,在坐标平面内是否存在一点
上一点,在坐标平面内是否存在一点 ,使得以
,使得以 、
、 、
、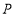 、
、 为顶点的四边形为菱形,若存在,求出此时
为顶点的四边形为菱形,若存在,求出此时 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
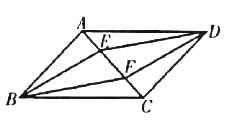
查看答案和解析>>【题目】如图,在
 中,点
中,点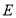 、
、 是对角线
是对角线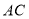 上两点,且
上两点,且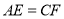 .
.
(1)求证:四边形
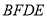 是平行四边形.
是平行四边形.(2)若
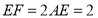 .
.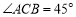 ,且
,且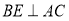 ,求
,求 的面积.
的面积.
相关试题

