【题目】如图,矩形![]() 中,
中,![]() ,对角线
,对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() 的平分线
的平分线![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() .
.
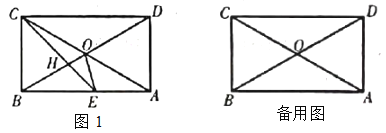
(l)求![]() 的度数;
的度数;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)求![]() .
.
参考答案:
【答案】(1)75°;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由矩形的性质可得AB∥CD,AO=CO=BO=DO,由角平分线的性质和平行线的性质可求BC=BE=BO,即可求解;
(2)过点H作FH⊥BC于F,由直角三角形的性质可得FH=![]() BF,BC=
BF,BC=![]() BF+BF=1,可求BH的长,由三角形面积公式可求△BCH的面积;
BF+BF=1,可求BH的长,由三角形面积公式可求△BCH的面积;
(3)过点C作CN⊥BO于N,由直角三角形的性质可求BC=![]() BF+BF=BO=BE,OH=OB-BH=
BF+BF=BO=BE,OH=OB-BH=![]() BF-BF,CN=
BF-BF,CN=![]() BC=
BC=![]() BF,即可求解.
BF,即可求解.
解:(1)∵四边形ABCD是矩形
∴AB∥CD,AO=CO=BO=DO,
∴∠DCE=∠BEC,
∵CE平分∠BCD
∴∠BCE=∠DCE=45°,
∴∠BCE=∠BEC=45°
∴BE=BC
∵∠BAC=30°,AO=BO=CO
∴∠BOC=60°,∠OBA=30°
∵∠BOC=60°,BO=CO
∴△BOC是等边三角形
∴BC=BO=BE,且∠OBA=30°
∴∠BOE=75°
(2)如图,过点H作FH⊥BC于F,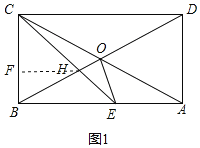
∵△BOC是等边三角形
∴∠FBH=60°,FH⊥BC
∴BH=2BF,FH=![]() BF,
BF,
∵∠BCE=45°,FH⊥BC
∴CF=FH=![]() BF
BF
∴BC=![]() BF+BF=1
BF+BF=1
∴BF=![]() ,
,
∴FH=![]() ,
,
∴S△BCH=![]() ×BC×FH=
×BC×FH=![]() ;
;
(3)如图,过点C作CN⊥BO于N,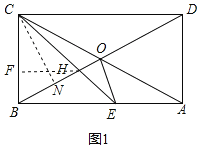
∵△BOC是等边三角形
∴∠FBH=60°,FH⊥BC
∴BH=2BF,FH=![]() BF,
BF,
∵∠BCE=45°,FH⊥BC
∴CF=FH=![]() BF
BF
∴BC=![]() BF+BF=BO=BE,
BF+BF=BO=BE,
∴OH=OB-BH=![]() BF-BF
BF-BF
∵∠CBN=60°,CN⊥BO
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 上部分点的横坐标
上部分点的横坐标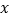 ,纵坐标
,纵坐标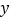 的对应值如下表:
的对应值如下表:x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数
 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是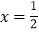 ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )A. ①② B. ①③ C. ①②③ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2
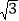 ,则∠A的度数为____________ .
,则∠A的度数为____________ .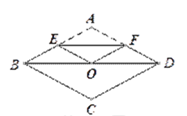
-
科目: 来源: 题型:
查看答案和解析>>【题目】为节约能源,优化电力资源配置,提高电力供应的整体效益,国家实行了错峰用电.某地区的居民用电,按白天时段和晚间时段规定了不同的单价.某户5月份白天时段用电量比晚间时段用电量多
 ,6月份白天时段用电量比5月份白天时段用电量少
,6月份白天时段用电量比5月份白天时段用电量少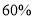 ,结果6月份的总用电量比5月份的总用电量多
,结果6月份的总用电量比5月份的总用电量多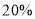 ,但6月份的电费却比5月份的电费少
,但6月份的电费却比5月份的电费少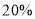 ,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )A.
 B.
B. C.
C. D.
D.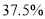
-
科目: 来源: 题型:
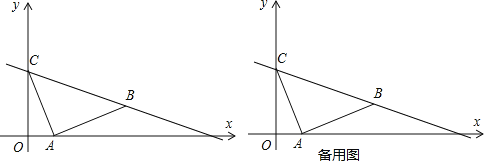
查看答案和解析>>【题目】如图,已知平面直角坐标系中,
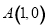 、
、 ,现将线段
,现将线段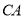 绕
绕 点顺时针旋转
点顺时针旋转 得到点
得到点 ,连接
,连接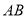 .
.
(1)求出直线
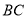 的解析式;
的解析式;(2)若动点
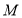 从点
从点 出发,沿线段
出发,沿线段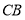 以每分钟
以每分钟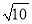 个单位的速度运动,过
个单位的速度运动,过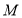 作
作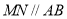 交
交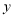 轴于
轴于 ,连接
,连接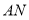 .设运动时间为
.设运动时间为 分钟,当四边形
分钟,当四边形 为平行四边形时,求
为平行四边形时,求 的值.
的值.(3)
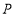 为直线
为直线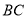 上一点,在坐标平面内是否存在一点
上一点,在坐标平面内是否存在一点 ,使得以
,使得以 、
、 、
、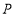 、
、 为顶点的四边形为菱形,若存在,求出此时
为顶点的四边形为菱形,若存在,求出此时 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
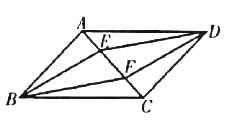
查看答案和解析>>【题目】如图,在
 中,点
中,点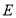 、
、 是对角线
是对角线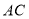 上两点,且
上两点,且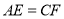 .
.
(1)求证:四边形
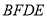 是平行四边形.
是平行四边形.(2)若
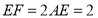 .
.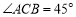 ,且
,且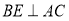 ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个.比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分
组别
听写正确的个数x
人数
A
0≤x<8
10
B
8≤x<16
15
C
16≤x<24
25
D
24≤x<32
m
E
32≤x<40
n
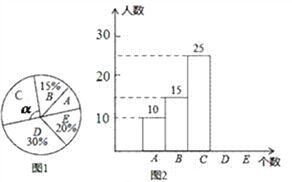
根据以上信息解决下列问题:
(1)本次共随机抽查了多少名学生,求出m,n的值并补全图2的条形统计图;
(2)求出图1中
 的度数;
的度数; (3)该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
相关试题

