【题目】《中国足球改革总体方案》提出足球要进校园,为了解某校学生对校园足球喜爱的情况,随机对该校部分学生进行了调查,将调查结果分为“很喜欢”、“较喜欢”、“一般”、“不喜欢”四个等级,并根据调查结果绘制成了如下两幅不完整的统计图;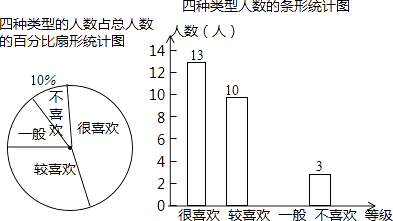
(1)一共调查了名学生,请补全条形统计图;
(2)在此次调查活动中,选择“一般”的学生中只有两人来自初三年级,现在要从选择“一般”的同学中随机抽取两人来谈谈各自对校园足球的感想,请用画树状图或列表法求选中的两人刚好都来自初三年级的概率.
参考答案:
【答案】
(1)30,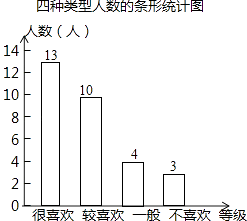
(2)解:用A,B分别表示来自初三年级的学生,C,D表示其他两个学生,
画树状图得:
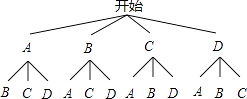
∵共有12种等可能的结果,选中的两人刚好都来自初三年级的有2种情况,
∴选中的两人刚好都来自初三年级的概率为: ![]() =
= ![]()
【解析】解:(1)根据题意得:一共调查的学生有:3÷10%=30(名);
调查结果为“一般”的人数:30﹣13﹣10﹣3=4(名).
故答案为:30;
补全统计图得:

(1)一共调查的学生人数=不喜欢足球的人数![]() 不喜欢足球的人数所占的百分比即可;调查结果为“一般”的人数=一共调查的学生人数-很喜欢足球的人数-较喜欢足球的人数-不喜欢足球的人数,根据计算补全条形统计图即可;
不喜欢足球的人数所占的百分比即可;调查结果为“一般”的人数=一共调查的学生人数-很喜欢足球的人数-较喜欢足球的人数-不喜欢足球的人数,根据计算补全条形统计图即可;
(2)用A,B分别表示来自初三年级的学生,C,D表示其他两个学生,根据题意画出树状图,知共有12种等可能的结果,选中的两人刚好都来自初三年级的有2种情况,根据概率公式计算即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) ﹣3
﹣3  ×(
×(  ﹣
﹣  )
)
(2) ﹣
﹣ 

(3)sin230°+2sin60°+tan45°﹣tan60°+cos230°. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=12cm,点C是直线AB上任意一点,M、N分别是AC、BC的中点,则线段MN=________cm.
-
科目: 来源: 题型:
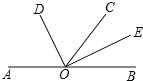
查看答案和解析>>【题目】如图,点A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)当∠BOE=25°时,求∠AOD的度数
(2)在图中找出∠COD的补角,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有小正方形的边长都为1,A、B、C都在格点上.
(1)过点C画直线AB的平行线(不写画法,下同);
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.
(3)线段_____的长度是点A到直线BC的距离;
(4)线段AG、AH的大小关系为AG_____AH.(填“>”或“<”或“=”),理由________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A,B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1 100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A,B两种商品很快售完,威丽商场决定再一次购进A,B两种商品共34件.如果将这34件商品全部售完后所得利润不低于4 000元,那么威丽商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
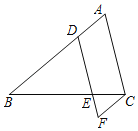
查看答案和解析>>【题目】如图,D,E分别是三角形ABC的边AB,BC上的点,DE∥AC,点F在DE的延长线上,且∠DFC=∠A.
(1)求证:AB∥CF;
(2)若∠ACF比∠BDE大40°,求∠BDE的度数.
相关试题

