【题目】(1)填空: ![]() ,
,![]() ,
, ![]() ,…
,…
(2)探索(1)中式子的规律,试写出第![]() 个等式,并说明第
个等式,并说明第![]() 个等式成立:
个等式成立:
(3)计算: ![]() .
.
参考答案:
【答案】(1)0,1,2;(2)第n个等式为:2n﹣2n﹣1=2n﹣1,(3)210﹣1.
【解析】试题分析:(1)根据乘方的运算法则计算即可;
(2)根据式子规律可得2n-2n-1=2n-1,然后利用提公因式2n-1可以证明这个等式成立;
(3)设题中的表达式为a,再根据同底数幂的乘法得出2a的表达式,相减即可.
试题解析:(1)21-20=2-1=20,22-21=4-2=21,23-22=8-4=22,
(2)第n个等式为:2n-2n-1=2n-1,
∵左边=2n-2n-1=2n-1(2-1)=2n-1,
右边=2n-1,
∴左边=右边,
∴2n-2n-1=2n-1;
(3)设a=20+21+22+23+…+28+29.①
则2a=21+22+23+…+28+29+210②
由②-①得:a=210-1,
∴20+21+22+23+…+28+29=210-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
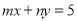 的两个解是
的两个解是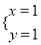 和
和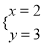
(1)求
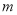 、
、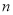 的值;
的值;(2)用含有
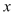 的代数式表示
的代数式表示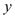 ;
;(3)若
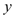 是不小于
是不小于 的负数,求
的负数,求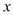 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】太仓港区道路绿化工程工地有大量货物需要运输,某车队有载重量为8吨和10吨的卡车共15辆,所有车辆运输一次能运输128吨货物.
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的扩大,车队需要一次运输货物170吨以上,为了完成任务,车队准备增购这两种卡车共5辆(两种车都购买),请写出所有可能的购车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值:2
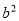 +(
+(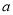 +
+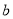 )(
)( 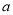 -2
-2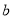 )-(
)-(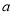 -
-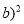 ,其中
,其中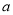 =-3,
=-3, 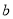 =
=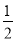 .
.(2)已知ab=-3,a+b=2.求下列各式的值:
①a2+b2;
②a3b+2a2b2 +ab3;
③a-b.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两名同学中选拔一个参加比赛,对他们的射击水平进行了测验,两个在相同条件下各射靶10次,命中的环数如下(单位:环)
甲:7,8,6,8,6,5,9,10,7,4
乙:9,5,7,8,6,8,7,6,7,7
(1)求
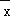 甲,
甲,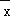 乙,S甲2,S乙2;
乙,S甲2,S乙2;(2)你认为该选拔哪名同学参加射击比赛?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的两边长分别是3和4,则第三边的长可能是( )
A. 1 B. 2 C. 7 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等式﹣2□(﹣2)=4成立,则“□”内的运算符号是( )
A. + B. ﹣ C. × D. ÷
相关试题

