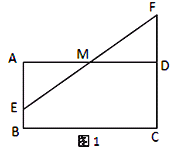
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.
(1)如图1,求证:AE=DF;
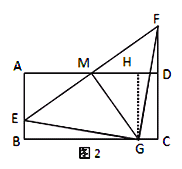
(2)如图2,若AB=2,过点M作 MG⊥EF交线段BC于点G,求证:△GEF是等腰直角三角形
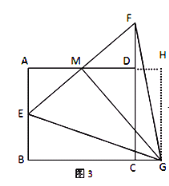
(3)如图3,若AB=2![]() ,过点M作 MG⊥EF交线段BC的延长线于点G.判断△GEF的形状,并说明理由.
,过点M作 MG⊥EF交线段BC的延长线于点G.判断△GEF的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)△GEF是等边三角形.证明见解析.
【解析】试题分析:(1)证明△AEM≌△DFM即可得;
(2)如图2,过点G作GH⊥AD于H,通过证明△AEM≌△HMG从而得出
ME=MG,∠EGM=45°,再由△AEM≌△DFM得ME=MF.从而得到△GEF是等腰直角三角形.
(3)如图3,△GEF是等边三角形.证明△AEM∽△HMG从而得![]() .
.
由tan∠MEG=![]() 得到∠MEG=60°. 由△AEM≌△DFM得到ME=MF.再由MG⊥EF得GE=GF.
得到∠MEG=60°. 由△AEM≌△DFM得到ME=MF.再由MG⊥EF得GE=GF.
从而确定△GEF是等边三角形.
试题解析:(1)如图1,在矩形ABCD中,∠EAM=∠FDM=90°,∠AME=∠FMD.
∵M是AD的中点,∴AM=DM,
∴△AEM≌△DFM(ASA).
∴AE=DF.
(2)如图2,过点G作GH⊥AD于H,
∴∠A=∠B=∠AHG=90°,∴四边ABGH为矩形,∴∠AME+∠AEM=90°,
∵MG⊥EF,∴∠GME=90°,∴∠AME+∠GMH=90°,∴∠AEM=∠GMH.
∵AD=4,M是AD的中点,∴AM=2,
∵四边ABGH为矩形,∴AB=HG=2,∴AM=HG,∴△AEM≌△HMG(AAS).
∴ME=MG,∴∠EGM=45°,
由(1)得△AEM≌△DFM,∴ME=MF.
∵MG⊥EF,∴GE=GF,∴∠EGF=2∠EGM=90°,∴△GEF是等腰直角三角形.
(3)如图3,△GEF是等边三角形.
过点G作GH⊥AD交AD延长线于点H,
∵∠A=∠B=∠AHG=90°,∴四边形ABGH是矩形. ∴GH=AB=![]() .
.
∵MG⊥EF,∴∠GME=90°.∴∠AME+∠GMH=90°.
∵∠AME+∠AEM=90°,∴∠AEM=∠GMH.
又∵∠A=∠GHM=90°,∴△AEM∽△HMG.∴ ![]() .
.
在Rt△GME中,∴tan∠MEG=![]() .
.
∴∠MEG=60°. 由(1)得△AEM≌△DFM.∴ME=MF.∵MG⊥EF, ∴GE=GF.
∴△GEF是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
 (k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中计算正确的是( )
A.(ab2)3=ab6 B.(3xy)2=6x2y2 C.(-2a2)2=-4a4 D.(a2b3)m=a2mb3m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为6,E是BC中点,将正方形边CD沿DE折叠到DF,将AD折叠,使AD与DF重合,折痕交AB于G,连接BF,CF,现在有如下4个结论:①G、F、E三点共线;②BG=4;③△BEF∽△CDF;④S△BFG=
 .
.在以上4个结论中,正确的有 ________________(填番号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为32,则OE的长等于( )
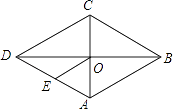
A.2
B.4
C.8
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】据报道:2013年底我国微信用户规模已到达6亿.以下是根据相关数据制作的统计图表的一部分:
2012年及2013年电话、电信、微信的人均使用时长统计表 单位:分钟分式
年份 电话
电话 短信
短信 微信
微信2012年
14.4
4.1
3.0
2013年
5.1
3.4
9.7
请根据以上信息,回答以下问题:
①从2012年到2013年微信的人均使用时长增加了________分钟;②在我国6亿微信用户中,经常使用户约为_________亿(结果精确到0.1);③从调查数学看,预计我国微信用户今后每年将以20%的增长率递增,请你估计两年后,我国微信用户的规模将到达_________亿.( )
A.6.7 2 8.5
B.9 1.8 8.64
C.6.7 1.5 8.64
D.6 1.8 8.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了九年级学生英语口语模拟测试,现从中随机抽取部分学生的口语模拟测试成绩统计如下.
口语成绩(分)
人数(人)
百分比(%)
26
8
16
27
24
28
15
29
m
30
5
根据上面提供的信息,回答下列问题:
(1)扇形统计图中的圆心角a= °;
(2)统计表中样本容量m= ;
(3)已知该校九年级共有400名学生,如果口语成绩达28分以上(含28分)为优秀,请估计该校九年级学生口语成绩达到优秀的总人数
相关试题

