【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图. 
请你根据以上的信息,回答下列问题:
(1)本次共调查了名学生,其中最喜爱体育的有人;
(2)在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是 .
(3)小李和小张在新闻、体育、动画三类电视节目中分别有一类是自己最喜爱的节目,请用树状图或列表法求两人恰好最喜爱同一类节目的概率.
参考答案:
【答案】
(1)50;10
(2)72°
(3)解:新闻、体育、动画三类电视节目分别记为A、B、C,
画树状图如下:
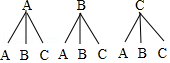
共有9种等可能的结果数,
两人恰好最喜爱同一类节目的概率为 ![]() =
= ![]() .
.
【解析】解:(1)本次共调查学生人数为4÷8%=50人,其中最喜爱体育的有50×(50%﹣30%)=10人, 所以答案是:50,10;
⑵在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是360°×(50%﹣30%)=72°,
所以答案是:72°;
【考点精析】通过灵活运用扇形统计图和条形统计图,掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=1,OC=
 ,在第二象限内,以原点O为位似中心将矩形AOCB放大为原来的
,在第二象限内,以原点O为位似中心将矩形AOCB放大为原来的  倍,得到矩形A1OC1B1 , 再以原点O为位似中心将矩形A1OC1B1放大为原来的
倍,得到矩形A1OC1B1 , 再以原点O为位似中心将矩形A1OC1B1放大为原来的  倍,得到矩形A2OC2B2…,以此类推,得到的矩形A100OC100B100的对角线交点的纵坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形A100OC100B100的对角线交点的纵坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣5)0+cos45°﹣|﹣
 |+
|+  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6
 米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.

(1)求证:点D在⊙O上;
(2)求证:F是AB的中点;
(3)若DE=4,求⊙O的半径和△BFH的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣2经过点A(1,0)和点B(4,0),与y轴交于点C.
附:阅读材料
法国弗朗索瓦韦达最早发现一元二次方程中根与系数的关系为:两根之和等于一次项系数与二次项系数之比的相反数,两根之积等于常数项羽二次项系数之比,人们称之为韦达定理.
即:设一元二次方程ax2+bx+c=0的两根为x1、x2 , 则:x1+x2=﹣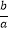 ,x1x2=
,x1x2= 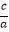 能灵活运用韦达定理,有时可以使解题更为简单.
能灵活运用韦达定理,有时可以使解题更为简单.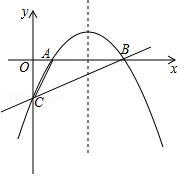
(1)求抛物线的解析式;
(2)以点A为圆心,作于直线BC相切的⊙A,求⊙A的面积;
(3)将直线BC向下平移n个单位后与抛物线交于点M、N,且线段MN=2CB,求直线MN的解析式及平移距离.
相关试题

