【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.
参考答案:
【答案】
(1)
如图1中,
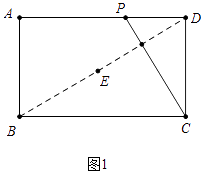
∵四边形ABCD是矩形,
∴∠ADC=∠A=90°,
∴∠DCP+∠CPD=90°,
∵∠CPD+∠ADB=90°,
∴∠ADB=∠PCD,
∵∠A=∠CDP=90°,
∴△ABD∽△DPC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PD= ![]() ,
,
∴t= ![]() s时,B、E、D共线.
s时,B、E、D共线.
(2)
如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.
作EQ⊥BC于Q,EM⊥DC于M.则EQ=3,CE=DC=4
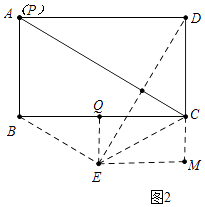
易证四边形EMCQ是矩形,
∴CM=EQ=3,∠M=90°,
∴EM= ![]() =
= ![]() =
= ![]() ,
,
∵∠DAC=∠EDM,∠ADC=∠M,
∴△ADC∽△DME,
![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AD=4 ![]() ,
,
如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3.
作EQ⊥BC于Q,延长QE交AD于M.则EQ=3,CE=DC=4
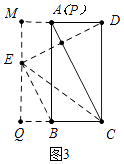
在Rt△ECQ中,QC=DM= ![]() =
= ![]() ,
,
由△DME∽△CDA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AD= ![]() ,
,
综上所述,在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,这样的m的取值范围 ![]() ≤m<4
≤m<4 ![]() .
.
【解析】(1)只要证明△ABD∽△DPC,可得 ![]() =
= ![]() ,由此求出PD即可解决问题;(2)分两种情形求出AD的值即可解决问题:①如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.②如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3;
,由此求出PD即可解决问题;(2)分两种情形求出AD的值即可解决问题:①如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.②如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3;
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与思考 婆罗摩笈多(Brahmagupta),是一位印度数学家和天文学家,书写了两部关于数学和天文学的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数概念及加减法运算仅晚于中国《九章算术》,而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及部分证明过程如下:
已知:如图1,四边形ABCD内接于⊙O,对角线AC⊥BD于点P,PM⊥AB于点M,延长MP交CD于点N,求证:CN=DN.
证明:在△ABP和△BMP中,∵AC⊥BD,PM⊥AB,
∴∠BAP+∠ABP=90°,∠BPM+∠MBP=90°.
∴∠BAP=∠BPM.
∵∠DPN=∠BPM,∠BAP=∠BDC.
∴…
(1)请你阅读婆罗摩笈多定理的证明过程,完成剩余的证明部分.
(2)已知:如图2,△ABC内接于⊙O,∠B=30°,∠ACB=45°,AB=2,点D在⊙O上,∠BCD=60°,连接AD,与BC交于点P,作PM⊥AB于点M,延长MP交CD于点N,则PN的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校课外兴趣小组从某市七年级学生中抽取2000人做了如下问卷调查,并将调查结果绘制成如图所示的两幅统计图.
问卷
你平时喝饮料吗?( )
A.不喝 B.喝
请选择B选项的同学回答下面问题:
请您减少喝饮料的数量,将节省下来的钱捐给希望工程,您愿意平均每月少喝( )
A.0瓶 B.1瓶
C.2瓶 D.2瓶以上

根据上述信息,解答下列问题:
(1)求条形图中n的值.
(2)如果每瓶饮料平均3元钱,“少喝2瓶以上”按少喝3瓶计算:
①这2000名学生一个月少喝饮料能节省多少钱捐给希望工程?
②按上述统计结果估计,该市七年级6万名学生一个月少喝饮料大约能节省多少钱捐给希望工程?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣4,0),B(0,4),在x轴上确定点M,使三角形MAB是等腰三角形,则M点的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的AB,BC,CA,OA,OB,OC组成.为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器.设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )

A.A→O→B
B.B→A→C
C.B→O→C
D.C→B→O -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点
 按如图方式叠放在一起,当
按如图方式叠放在一起,当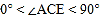 且点
且点 在直线
在直线 的上方时,解决下列问题:(友情提示:
的上方时,解决下列问题:(友情提示: ,
, ,
, .
.
(1)①若
 ,则
,则 的度数为 ;
的度数为 ;②若
 ,则
,则 的度数为 ;
的度数为 ;(2)由(1)猜想
 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出
 的角度所有可能的值(不必说明理由);若不存在,请说明理由.
的角度所有可能的值(不必说明理由);若不存在,请说明理由.
相关试题

