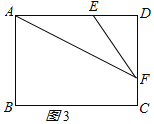
【题目】如图,在一张长为7cm,宽为5cm的矩形纸片上,现在剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的的高为_____________。

参考答案:
【答案】4或![]() 或
或![]()
【解析】
分三种情况进行讨论:(1)△AEF为等腰直角三角形,得出AE上的高为AF=4;
(2)利用勾股定理求出AE边上的高BF即可;
(3)求出AE边上的高DF即可
解:分三种情况:
(1)当AE=AF=4时,
如图1所示:
△AEF的腰AE上的高为AF=4;
(2)当AE=EF=4时,
如图2所示:
则BE=5-4=1,
BF=![]() ;
;
(3)当AE=EF=4时,
如图3所示:
则DE=7-4=3,
DF=![]() ,
,
故答案为4或![]() 或
或![]() .
.


-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=|a-b|,线段AB的中点表示的数为
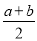

(问题情境)如图1,已知数轴上有三点
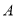 、
、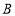 、
、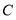 ,
,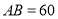 ,点
,点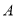 对应的数是
对应的数是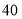 .
.(综合运用)(1)点B表示的数是__________.
(2)若
 ,求点
,求点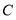 到原点的距离.
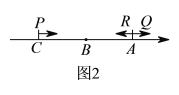
到原点的距离.(3)如图2,在(2)的条件下,动点
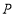 、
、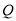 两点同时从
两点同时从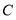 、
、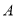 出发向右运动,同时动点
出发向右运动,同时动点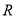 从点
从点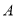 向左运动,已知点
向左运动,已知点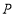 的速度是点
的速度是点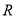 的速度的
的速度的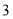 倍,点
倍,点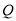 的速度是点
的速度是点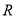 的速度
的速度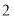 倍少
倍少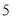 个单位长度/秒.经过
个单位长度/秒.经过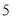 秒,点
秒,点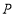 、
、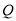 之间的距离与点
之间的距离与点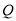 、
、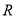 之间的距离相等,求动点
之间的距离相等,求动点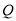 的速度;
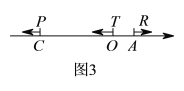
的速度;(4)如图3,在(2)的条件下,
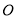 表示原点,动点
表示原点,动点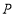 、
、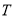 分别从
分别从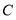 、
、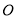 两点同时出发向左运动,同时动点
两点同时出发向左运动,同时动点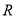 从点
从点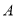 出发向右运动,点
出发向右运动,点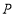 、
、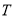 、
、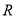 的速度分别为
的速度分别为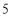 个单位长度/秒,
个单位长度/秒,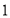 个单位长度/秒、
个单位长度/秒、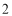 个单位长度/秒,在运动过程中,如果点
个单位长度/秒,在运动过程中,如果点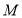 为线段
为线段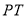 的中点,点
的中点,点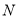 为线段
为线段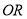 的中点.请问
的中点.请问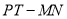 的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.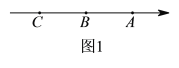
-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝“春节”,市政府决定在市政广场上增一排灯花,其设计由以下图案逐步演变而成,其中圆圈代表灯花中的灯泡,n代表第n次演变过程,s代表第n次演变后的灯泡的个数,仔细观察下列演变过程,当n=7时,s=( ).
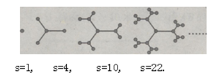
A.162B.176C.190D.214
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“”规定一种新运算:对于任意有理数a和b,规定ab=ab+2ab+a. 如:13=1×3+2×1×3+1=16
(1)求3(﹣1)的值;
(2)若(a+1)2=36,求a的值;
(3)若m=2x,n=(
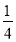 x)3(其中x为有理数),试比较m、n的大小.
x)3(其中x为有理数),试比较m、n的大小. -
科目: 来源: 题型:
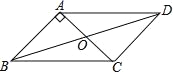
查看答案和解析>>【题目】已知:如图,在ABCD中,对角线AC,BD交于点O,AB⊥AC,AB=1,BC=
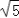 .
.(1)求平行四边形ABCD的面积S□ABCD;
(2)求对角线BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.

相关试题

