搜索
【题目】如图正方形网格中的△ABC，若小方格边长为1，请你根据所学的知识。
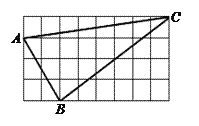
（1）求△ABC的面积；
（2）判断△ABC是什么形状？并说明理由。
参考答案：
【答案】（1）13；（2）△ABC是直角三角形
【解析】试题分析：（1）用矩形的面积减去三个小三角形的面积即可求出△ABC的面积；（2）根据勾股定理求得△ABC各边的长，再利用勾股定理的逆定理即可得△ABC的形状．
试题解析：
（1）△ABC的面积=4×8－1×8÷2－2×3÷2－6×4÷2=13，故△ABC的面积为13；
（2）∵正方形小方格边长为1，
∴AC=
， 
， 
。
∵在△ABC 中，AB2+BC2=13+52=65，AC2=65，
∴AB2+BC2=AC2，
∴网格中的△ABC是直角三角形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表：
x
﹣1
0
0.5
2
y
﹣1
2
3.75
2
①ac＜0；
②当x＞1时，y的值随x值的增大而减小；
③x=2是方程ax2+（b﹣1）x+c=0的一个根；
④当﹣1＜x＜2时，ax2+（b﹣1）x+c＞0．
上述结论中正确的有（ ）个．
A．1 B．2 C．3 D．4
-
科目： 来源： 题型：
查看答案和解析>>【题目】有一个等腰三角形，三边长分别为3x－2，4x－3，6－2x，求这个等腰三角形的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】分析探索题：细心观察如图，认真分析各式，然后解答问题。
OA22=(
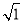)2＋1＝2 
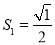；OA32=(
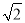)2＋1＝3 
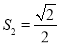；OA42=(
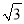)2＋1＝4 
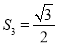…填空：（1）请写出含有n（n为正整数）的等式Sn= ；
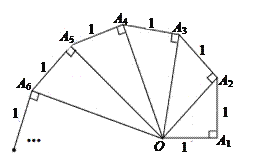
（2）推算出OA10= 。
（3）求S12+S22+S32+…+S102的值。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点A，B在半径为1的⊙O上，∠AOB=60°，延长OB至C，过点C作直线OA的垂线记为l，则下列说法正确的是（ ）
A．当BC等于0.5时，l与⊙O相离
B．当BC等于2时，l与⊙O相切
C．当BC等于1时，l与⊙O相交
D．当BC不为1时，l与⊙O不相切
-
科目： 来源： 题型：
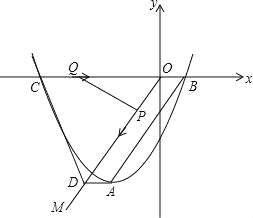
查看答案和解析>>【题目】如图，顶点为A的抛物线y=a（x+2）2﹣4交x轴于点B（1，0），连接AB，过原点O作射线OM∥AB，过点A作AD∥x轴交OM于点D，点C为抛物线与x轴的另一个交点，连接CD．
（1）求抛物线的解析式、直线AB的解析式；
（2）若动点P从点O出发，以每秒1个单位长度的速度沿线段OD向点D运动，同时动点Q从点C出发，以每秒2个单位长度的速度沿线段CO向点O运动，当其中一个点停止运动时另一个点也随之停止运动．
问题一：当t为何值时，△OPQ为等腰三角形？
问题二：当t为何值时，四边形CDPQ的面积最小？并求此时PQ的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在同一平面内，不互相重合的两条直线位置关系有种，它们是 ， ．
相关试题
