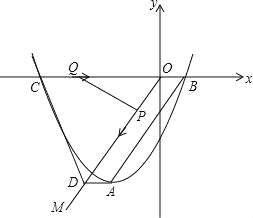
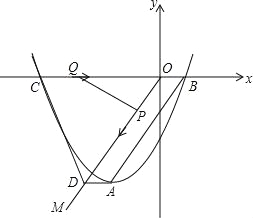
【题目】如图,顶点为A的抛物线y=a(x+2)2﹣4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
(1)求抛物线的解析式、直线AB的解析式;
(2)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.
问题一:当t为何值时,△OPQ为等腰三角形?
问题二:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
参考答案:
【答案】(1)![]() (2)PQ=
(2)PQ=![]()
【解析】
试题分析:(1)把点B坐标代入抛物线解析式即可求出a的值,写出顶点A的坐标,运用待定系数法即可求出直线AB的解析式;
(2)问题一,先用t表示OQ,OP的长度,再分类列出方程求解即可得出t的值,问题二:写出四边形面积关于t的二次函数,求最大值即可.
试题解析:(1)由顶点为A的抛物线y=a(x+2)2﹣4交x轴于点B(1,0)可得:
0=a(1+2)2﹣4,解得:a=![]() ,
,
∴抛物线的解析式:![]() ,
,
顶点A(﹣2,﹣4),
设直线AB:y=bx+k,带入点A,B两点坐标得:![]() ,
,
解得: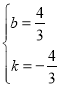 ,
,
∴直线AB的解析式:![]() ,
,
(2)如图:
∵OD∥AB,所以得直线OD:![]() ,
,
∵AD∥x轴,解得点D(﹣3,﹣4),
解得OD=5,tan∠COD=![]() ,sin∠COD=
,sin∠COD=![]() ,cos∠COD=
,cos∠COD=![]() ,
,
把y=0带入抛物线解析式得: ![]() ,
,
解得:x=1,或x=﹣5,
所以点C(﹣5,0),
∴OC=5,
由2t≤5,得t≤2.5,
OP=t,OQ=5﹣2t,
当OP=OQ时,有:t=5﹣2t,解得t=![]() ,
,
当OQ=QP时,有:t=2(5﹣2t)×![]() ,解得t=
,解得t=![]() ,
,
当QP=OP时,有:5﹣2t=2t×![]() ,解得t=
,解得t=![]() ,
,
综上所述,当t为![]() ,
,![]() ,
,![]() 时,△OPQ为等腰三角形;
时,△OPQ为等腰三角形;
四边形CDPQ的面积=![]() =
=![]() ×5×4﹣
×5×4﹣![]() ×(5﹣2t)×t×
×(5﹣2t)×t×![]() =
=![]() ,
,
所以当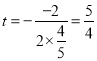 时,四边形CDPQ的面积有最小值,
时,四边形CDPQ的面积有最小值,
此时,OQ=![]() ,OP=
,OP=![]() ,sin∠COD=
,sin∠COD=![]() ,cos∠COD=
,cos∠COD=![]() ,
,
可求得PQ=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分析探索题:细心观察如图,认真分析各式,然后解答问题。
OA22=(
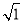 )2+1=2
)2+1=2 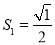 ;
;OA32=(
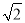 )2+1=3
)2+1=3 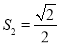 ;
;OA42=(
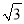 )2+1=4
)2+1=4 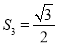 …
…填空:(1)请写出含有n(n为正整数)的等式Sn= ;
(2)推算出OA10= 。
(3)求S12+S22+S32+…+S102的值。
-
科目: 来源: 题型:
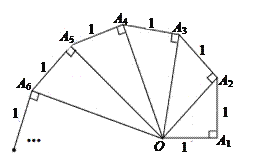
查看答案和解析>>【题目】如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识。
(1)求△ABC的面积;
(2)判断△ABC是什么形状?并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )

A.当BC等于0.5时,l与⊙O相离
B.当BC等于2时,l与⊙O相切
C.当BC等于1时,l与⊙O相交
D.当BC不为1时,l与⊙O不相切
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,不互相重合的两条直线位置关系有种,它们是 , .
-
科目: 来源: 题型:
查看答案和解析>>【题目】《济南市人口发展“十三五“规划》近日出炉,根据规划,到2020年全市常住人口将达到70万人,城区常住人口规模达500万人以上,迈入特大城市行列,770万这个数用科学记数法表示为( )
A. 77×105 B. 7.7×105 C. 7.7×106 D. 0.77×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm。

求:(1)FC的长;
(2)EF的长。
相关试题

