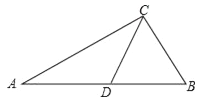
【题目】如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=![]() ,tanA=
,tanA=![]() ,BC=2
,BC=2![]() ,求边AB的长和cos∠CDB的值.
,求边AB的长和cos∠CDB的值.
参考答案:
【答案】边AB的长为6,cos∠CDB=![]()
【解析】整体分析:
过点C作CE⊥AB于点E,解Rt△BCE,求CE,BE,在Rt△ACE中,由CE,tanA的值求AE,则可求AB;在Rt△CDE中,求出DE,CD,由余弦的定义求cos∠CDB.
解:过点C作CE⊥AB于点E,
在Rt△BCE中,∵BC=![]() ,sinB=
,sinB=![]() ,
,
∴CE=BC·sinB=![]() ×
×![]() =2,∴BE=
=2,∴BE=![]() =
=![]() =2,
=2,
在Rt△ACE中,∵tanA=![]() ,
,
∴AE=![]() =
=![]() =4,∴AB=AE+BE=4+2=6,
=4,∴AB=AE+BE=4+2=6,
∵CD是边AB上的中线,∴BD=![]() AB=3,∴DE=BD﹣BE=1,
AB=3,∴DE=BD﹣BE=1,
在Rt△CDE中,∵CD=![]() =
=![]() =
=![]() ,
,
∴cos∠CDB=![]() =
=![]() =
=![]() .
.
故边AB的长为6,cos∠CDB=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在互联网技术的影响下,幸福新村的村民小刘在网上销售苹果,原计划每天卖100千克,但实际每天的销量与计划销量相比有出入,如表是某周的销售情况(超额记为正,不足记为负.单位:千克):
星期
一
二
三
四
五
六
日
与计划量的差值
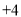
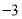
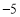
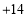
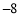
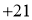
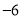
(1)根据表中的数据可知前三天共卖出___________千克;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售多少千克?
(3)若每千克按5元出售,每千克苹果的运费为1元,那么小刘本周一共收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
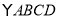 中,AE
中,AE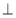 BC于点E,延长BC至点F,点使
BC于点E,延长BC至点F,点使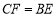 ,连接AF、DE、DF。
,连接AF、DE、DF。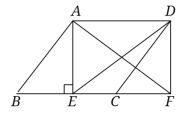
(1)求证:四边形AEFD是矩形;
(2)若
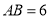 ,
,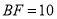 ,,求AE的长。
,,求AE的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】实验中学地理社团学生在5名地理老师的带领下去黄河风景区进行参观考察,景区的门票为每人40元.现有两种优惠方案.甲方案:带队教师免费,学生按9折收费;乙方案:师生都8折收费.
(1)若有
 名学生,用代数式表示两种优惠方案各需多少元?
名学生,用代数式表示两种优惠方案各需多少元?(2)当
 为何值时,两种优惠方案收费相同?
为何值时,两种优惠方案收费相同?(3)当
 时,采用哪种方案优惠?
时,采用哪种方案优惠? -
科目: 来源: 题型:
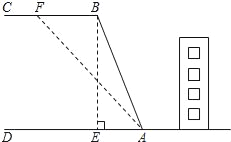
查看答案和解析>>【题目】如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:
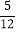 ,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a2﹣ab+b2)﹣(3a2+ab+b2),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+
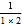 a2)+(3b+
a2)+(3b+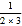 a2)+…+(9b+
a2)+…+(9b+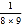 a2)的值.
a2)的值. -
科目: 来源: 题型:
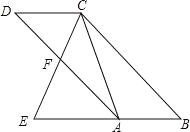
查看答案和解析>>【题目】如图,已知:四边形ABCD是平行四边形,点E在边BA的延长线上,CE交AD于点F,∠ECA=∠D
(1)求证:△EAC∽△ECB;
(2)若DF=AF,求AC:BC的值.
相关试题

