【题目】如图,△ABE为等腰直角三角形,∠ABE=90°,BC=BD,∠FAD=30°.

(1)求证:△ABC≌△EBD;
(2)求∠AFE的度数.
参考答案:
【答案】(1)见解析;(2)90°
【解析】
试题分析:(1)根据等腰直角三角形的性质得到AB=BE,根据邻补角的定义得到∠ABE=∠DBE=90°,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到∠BAC=∠BED,根据三角形的内角和得到∠BED+∠D=90°,等量代换得到∠BAC+∠D=90°,即可得到结论.
(1)证明:∵△ABE为等腰直角三角形,
∴AB=BE,
∵∠ABE=90°,
∴∠ABE=∠DBE=90°,
在△ABC与△BDE中,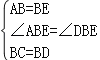 ,
,
∴△ABC≌△EBD;
(2)解:∵△ABC≌△EBD,
∴∠BAC=∠BED,
∵∠BED+∠D=90°,
∴∠BAC+∠D=90°,
∴∠AFD=90°,
∴∠AFE=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于点和A(﹣1,0)和点B(4,0),与y轴交于点C(0,2).

(1)求抛物线解析式;
(2)点P是抛物线BC段上一点,PD⊥BC,PE∥y轴,分别交BC于点D、E.当DE=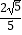 时,求点P的坐标;
时,求点P的坐标;
(3)M是平面内一点,将符合(2)条件下的△PDE绕点M沿逆时针方向旋转90°后,点P,D,E的对应点分别是P′、D′、E′.设P′E′的中点为N,当抛物线同时经过D′与N时,求出D′的横坐标. -
科目: 来源: 题型:
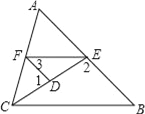
查看答案和解析>>【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的函数关系式为
 ,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,
,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,
(1)求直线l2的解析式;
(2)求△ADC的面积;
(3)在直线l2上存在一点F(不与C重合),使得△ADF和△ADC的面积相等,请求出F点的坐标;
(4)在x轴上是否存在一点E,使得△BCE的周长最短?若存在请求出E点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中装有三张卡片,分别标有数字1,2,3,这些卡片除数字不同外其余均相同.小吉从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求两次抽取的卡片上数字之和为奇数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场甲、乙、丙三名业务员5个月的销售额(单位:万元)如下表:
月份
销售额
人员第1月
第2月
第3月
第4月
第5月
甲
7.2
9.6
9.6
7.8
9.3
乙
5.8
9.7
9.8
5.8
9.9
丙
4
6.2
8.5
9.9
9.9
(1)根据上表中的数据,将下表补充完整:统计值
数值
人员平均数(万元)
中位数(万元)
众数(万元)
甲
9.3
9.6
乙
8.2
5.8
丙
7.7
8.5
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A、1.5小时以上;B、1~1.5小时;C、0.5~1小时;D、0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下?

相关试题

