【题目】如图,直线l1的函数关系式为![]() ,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,
,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,

(1)求直线l2的解析式;
(2)求△ADC的面积;
(3)在直线l2上存在一点F(不与C重合),使得△ADF和△ADC的面积相等,请求出F点的坐标;
(4)在x轴上是否存在一点E,使得△BCE的周长最短?若存在请求出E点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=﹣x+4;(2)6;(3)(6,﹣2);(4)见解析
【解析】
试题分析:(1)利用待定系数法即可直接求得l2的函数解析式;
(2)首先解两条之间的解析式组成的方程组求得C的坐标,然后利用三角形的面积公式即可求解;
(3)△ADF和△ADC的面积相等,则F的纵坐标与C的总坐标一定互为相反数,代入l2的解析式即可求解;
(4)求得C关于x轴的对称点,然后求得经过这个点和B点的直线解析式,直线与x轴的交点就是E.
解:(1)设l2的解析式是y=kx+b,
根据题意得:![]() ,解得:
,解得: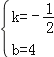 ,
,
则函数的解析式是:y=﹣x+4;
(2)在![]() 中令y=0,解得:x=﹣2,则D的坐标是(﹣2,0).
中令y=0,解得:x=﹣2,则D的坐标是(﹣2,0).
解方程组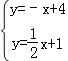 ,
,
解得:![]() ,
,
则C的坐标是(2,2).
则S△ADC=![]() ×6×2=6;
×6×2=6;
(3)把y=﹣2代入y=﹣x+4,得﹣2=﹣x+4,
解得:x=6,
则F的坐标是(6,﹣2);
(4)C(2,2)关于x轴的对称点是(2,﹣2),
则设经过(2,﹣2)和B的函数解析式是y=mx+n,
则![]() ,
,
解得:![]() ,
,
则直线的解析式是y=3x+8.
令y=0,则3x+8=0,解得:x=﹣![]() .
.
则E的坐标是(﹣![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】点C在直线AB上,AC=10cm,CB=8cm,点M、N分别是AC、BC的中点,则线段MN的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于点和A(﹣1,0)和点B(4,0),与y轴交于点C(0,2).

(1)求抛物线解析式;
(2)点P是抛物线BC段上一点,PD⊥BC,PE∥y轴,分别交BC于点D、E.当DE=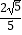 时,求点P的坐标;
时,求点P的坐标;
(3)M是平面内一点,将符合(2)条件下的△PDE绕点M沿逆时针方向旋转90°后,点P,D,E的对应点分别是P′、D′、E′.设P′E′的中点为N,当抛物线同时经过D′与N时,求出D′的横坐标. -
科目: 来源: 题型:
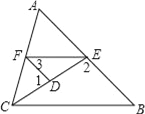
查看答案和解析>>【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABE为等腰直角三角形,∠ABE=90°,BC=BD,∠FAD=30°.

(1)求证:△ABC≌△EBD;
(2)求∠AFE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中装有三张卡片,分别标有数字1,2,3,这些卡片除数字不同外其余均相同.小吉从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求两次抽取的卡片上数字之和为奇数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场甲、乙、丙三名业务员5个月的销售额(单位:万元)如下表:
月份
销售额
人员第1月
第2月
第3月
第4月
第5月
甲
7.2
9.6
9.6
7.8
9.3
乙
5.8
9.7
9.8
5.8
9.9
丙
4
6.2
8.5
9.9
9.9
(1)根据上表中的数据,将下表补充完整:统计值
数值
人员平均数(万元)
中位数(万元)
众数(万元)
甲
9.3
9.6
乙
8.2
5.8
丙
7.7
8.5
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
相关试题

