【题目】如图,抛物线y= ![]() x2+
x2+ ![]() x﹣2与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E,若点C(4,n)在抛物线上,且CE∥x轴.
x﹣2与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E,若点C(4,n)在抛物线上,且CE∥x轴. 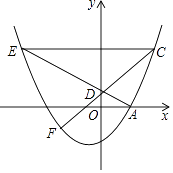
(1)求m,n的值;
(2)连结CD并延长交抛物线于点F,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)解:∵抛物线上x=4时,y= ![]() ×16+
×16+ ![]() ×4﹣2=4,
×4﹣2=4,
∴点C坐标为(4,4),n=4,
∵当y= ![]() x2+
x2+ ![]() x﹣2=4时,解得:x=4或﹣6,
x﹣2=4时,解得:x=4或﹣6,
∴点E坐标为(﹣6,4),
∵当y= ![]() x2+
x2+ ![]() x﹣2=0时,x=2或﹣4,
x﹣2=0时,x=2或﹣4,
∴点A坐标为(2,0),
设直线AE解析式为y=kx+b,则 ![]() ,
,
解得:k=﹣ ![]() ,b=1,
,b=1,
∴直线AE解析式为y=﹣ ![]() x+1,
x+1,
当x=0时,y=1,∴点D坐标为(0,1)
(2)解:设直线CD解析式为y=kx+b,
则代入C、D点得: ![]() ,
,
解得:k= ![]() ,b=1,
,b=1,
∴直线CD解析式为y= ![]() x+1,
x+1,
当y= ![]() x2+
x2+ ![]() x﹣2=
x﹣2= ![]() x+1时,化简得:x2﹣x﹣12=0,
x+1时,化简得:x2﹣x﹣12=0,
解得:x=4或﹣3,
∴点F坐标为(﹣3,﹣ ![]() ),
),
∴DF=  =
= ![]() ,
,
CD= ![]() =5,
=5,
∴ ![]() =
= ![]() =
= ![]()
【解析】(1)将点C横坐标代入抛物线解析式即可求得n的值,根据n的值可以求得点E的坐标,即可求得点A坐标,即可求得直线AE解析式,即可解题;(2)易求得直线CD解析式,即可求得点F坐标,即可求得DF、CD的长,即可解题.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知单位长度为1的方格中有三角形ABC.
(1)请画出三角形ABC向上平移3格再向右平移2格所得的三角形A′B′C′;
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标.
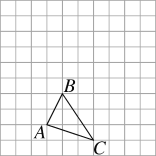
-
科目: 来源: 题型:
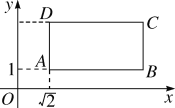
查看答案和解析>>【题目】如图,长方形ABCD在坐标平面内,点A的坐标是A(
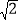 ,1),且边AB,CD与x轴平行,边AD,BC与y轴平行,AB=4,AD=2.
,1),且边AB,CD与x轴平行,边AD,BC与y轴平行,AB=4,AD=2.(1)求B,C,D三点的坐标;
(2)怎样平移,才能使A点与原点O重合?
-
科目: 来源: 题型:
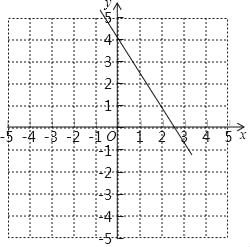
查看答案和解析>>【题目】点A(0,4),B(2,1)是直角坐标系中的两个点.
(1)请在平面直角坐标系中描出A,B两点,并画出直线AB;
(2)写出B点关于y轴的对称点B′的坐标 ;
(3)求出直线AB与x轴的交点坐标 .
-
科目: 来源: 题型:
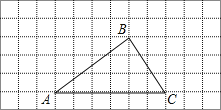
查看答案和解析>>【题目】在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.△ABC的顶点A、B、C都在格点上.
(1)过B作AC的平行线BD.
(2)作出表示B到AC的距离的线段BE.
(3)线段BE与BC的大小关系是:BE BC(填“>”、“<”、“=”).
(4)△ABC的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解密数学魔术:魔术师请观众心想一个数,然后将这个数按以下步骤操作:

魔术师能立刻说出观众想的那个数.
(1)如果小玲想的数是
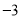 ,请你通过计算帮助她告诉魔术师的结果;
,请你通过计算帮助她告诉魔术师的结果;(2)如果小明想了一个数计算后,告诉魔术师结果为85,那么魔术师立刻说出小明想的那个数是:__________;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数.若设观众心想的数为
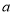 ,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?
相关试题

