【题目】如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)当M点在(何处)时,AM+CM的值最小;
(2)当AM+EM的值最小时,∠BCM=°.
(3)①求证:△AMB≌△ENB;②当M点在何处时,AM+BM+CM的值最小,并说明理由.
参考答案:
【答案】
(1)BD的中点
(2)15
(3)解:①∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°,
∵∠MBN=60°,
∴∠MBN-∠ABN=∠ABE-∠ABN,
即∠BMA=∠NBE,
又∵MB=NB,
∴△AMB≌△ENB(SAS);
②如图,连接CE,
当M点位于BD与CE的交点处时,AM+BM+CM的值最小,
理由如下:连接MN,
由(1)知,△AMB≌△ENB,
∴AM=EN,
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形,
∴BM=MN,
∴AM+BM+CM=EN+MN+CM,
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
【解析】(1)①当M点落在BD的中点时,A.M、C三点共线,AM+CM的值最小;
( 2 )如图: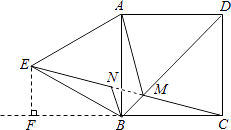
连接CE,当M点位于BD与CE的交点处时,AM+EM的值最小,
过E作EF⊥BC于点F,四边形ABCD是正方形,△ABE是等边三角形,
∴BE=BC,∠EBF=∠ABF-∠ABE=90°-60°=30°,
∴∠BCM= ![]() ∠EBF=15°;
∠EBF=15°;
(1)根据两点之间线段最短,①当M点落在BD的中点时,A.M、C三点共线,AM+CM的值最小。
(2)连接CE,当M点位于BD与CE的交点处时,AM+EM的值最小,过E作EF⊥BC于点F,根据已知ABCD是正方形,△ABE是等边三角形,得出BE=BC,∠EBF=30°,再根据三角形外角的性质,求出∠BCM的度数即可。
(3)①根据等边三角形的性质得出BA=BE,∠ABE=60°,根据∠MBN=60°,然后证明△AMB≌△ENB即可;②连接CE,当M点位于BD与CE的交点处时,AM+BM+CM的值最小,再根据已知及①的结论证明AM=EN,BM=MN,将AM、BM、CM转化到同一条线段上,根据两点之间线段最短,即可得出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上.

(1)①若将线段AB绕点O逆时针旋转90°得到线段A1B1 , 试在图中画出线段A1B1 .
②若线段A2B2与线段A1B1关于y轴对称,请画出线段A2B2 .
(2)若点P是此平面直角坐标系内的一点,当点A、B1、B2、P四边围成的四边形为平行四边形时,请你直接写出点P的坐标(写出一个即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足若
 ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.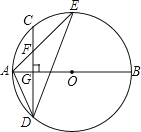
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求tan∠E的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数
 的图象和矩形ABCD在第一象限,AD平行于
的图象和矩形ABCD在第一象限,AD平行于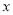 轴,且AB=2,AD=4,点A的坐标为(2,6).
轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出B、C、D三点的坐标.
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点M(a-3,a+4),点N(5,9),若MN∥y轴,则a=____.
相关试题

