【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( ) 
A.![]()
B.6
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:连接BC′,
∵旋转角∠BAB′=45°,∠BAD′=45°,
∴B在对角线AC′上,
∵B′C′=AB′=3,
在Rt△AB′C′中,AC′= ![]() =3
=3 ![]() ,∴B′C=3
,∴B′C=3 ![]() ﹣3,在等腰Rt△OBC′中,OB=BC′=3
﹣3,在等腰Rt△OBC′中,OB=BC′=3 ![]() ﹣3,
﹣3,
在直角三角形OBC′中,OC= ![]() (3
(3 ![]() ﹣3)=6﹣3
﹣3)=6﹣3 ![]() ,∴OD′=3﹣OC′=3
,∴OD′=3﹣OC′=3 ![]() ﹣3,
﹣3,
∴四边形ABOD′的周长是:2AD′+OB+OD′=6+3 ![]() ﹣3+3
﹣3+3 ![]() ﹣3=6
﹣3=6 ![]() .
.
故选:A.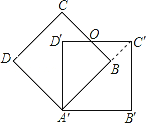
由边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,利用勾股定理的知识求出BC′的长,再根据等腰直角三角形的性质,勾股定理可求BO,OD′,从而可求四边形ABOD′的周长.本题考查了旋转的性质、正方形的性质以及等腰直角三角形的性质.此题难度适中,注意连接BC′构造等腰Rt△OBC′是解题的关键,注意旋转中的对应关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣5(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.

(1)求这条抛物线的表达式;
(2)联结AB、BC、CD、DA,求四边形ABCD的面积;
(3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
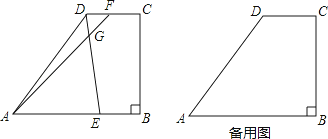
(1)求线段CD的长;
(2)如果△AEC是以EG为腰的等腰三角形,求线段AE的长;
(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1,l2交于点C.
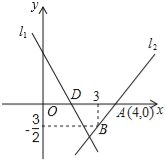
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在l2上存在异于点C的另一点P,使得△ADP与△ADC面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
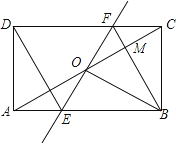
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是双曲线
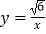 在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线 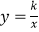 上运动,则k的值是
上运动,则k的值是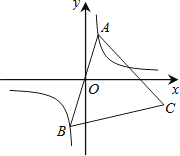
相关试题

