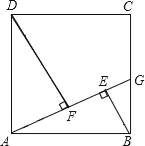
【题目】如图,在边长为4的正方形ABCD中,点G是BC边上的任意一点(不同于端点B、C),连接AG,过B、D两点作BE⊥AG,DF⊥AG,垂足分为E、F.
(1)求证:△ABE≌△DAF;
(2)若△ADF的面积为1,试求|BE﹣DF|的值.
参考答案:
【答案】(1)证明见解析(2)2![]()
【解析】试题分析:
(1)由已知条件易得:∠DFA=∠AEB=∠DAB=90°,从而可得∠ADF+∠DAF=∠DAF+∠BAE=90°,由此即可得到∠ADF=∠BAE,结合正方形ABCD中AD=AB即可证得△ABE≌△DAF;
(2)设AF=a,DF=b,则由△ADF的面积为1可得![]() ,即可得到
,即可得到![]() ;由正方形的边长为4在Rt△ADF中可得:
;由正方形的边长为4在Rt△ADF中可得: ![]() ,由此即可得到
,由此即可得到![]() ,即可解得
,即可解得![]() 的值,从而可由|BE﹣DF|=|AF﹣DF|求出所求的值.
的值,从而可由|BE﹣DF|=|AF﹣DF|求出所求的值.
试题解析:
(1)在正方形ABCD中,∠DAB=90°,AB=AD,
∴∠DAF+∠BAE=90°,
∵DF⊥AG,BE⊥AG,
∴∠AFD=∠BEA=90°,∠DAF+∠ADF=90°,
∴∠BAE=∠ADF,
在△ABE和△DAF中, 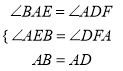 ,
,
∴△ABE≌△DAF(AAS);

(2)∵△ABE≌△DAF,
∴BE=AF,
设AF=a,DF=b,
∵△ADF的面积为1,
∴![]() AFDF=1,即
AFDF=1,即![]() ab=1,
ab=1,
∴ ab=2,
在Rt△ADF中,根据勾股定理得,AF2+DF2=AD2,即a2+b2=42=16,
∴(a﹣b)2=a2﹣2ab+b2=16﹣4=12,
∴|a﹣b|=![]() ,即|AF﹣DF|=|BE﹣DF|=
,即|AF﹣DF|=|BE﹣DF|=![]() .
.
-
科目: 来源: 题型:
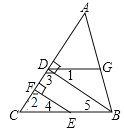
查看答案和解析>>【题目】如图,BD⊥AC,EF⊥AC,D、F分别是垂足,且∠1=∠4,试说明:∠ADG=∠C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.

(1)求该一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积。
-
科目: 来源: 题型:
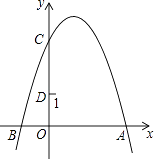
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体的质量(kg)
0
1
2
3
4
5
弹簧的长度(cm)
12
12.5
13
13.5
14
14.5
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度怎样变化?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
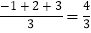 ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4
 ,
, 
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

相关试题

