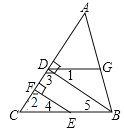
【题目】如图,BD⊥AC,EF⊥AC,D、F分别是垂足,且∠1=∠4,试说明:∠ADG=∠C.
参考答案:
【答案】说明见解析.
【解析】先由垂直的定义得到:∠2=∠3,然后由同位角相等,两直线平行得到:EF∥BD,再由两直线平行,同位角相等得到:∠4=∠5,然后根据等量代换得到:∠1=∠5,再根据内错角相等,两直线平行得到:DG∥BC,最后由两直线平行,同位角相等即可证∠ADG=∠C.
∵BD⊥AC,EF⊥AC(已知)
∴∠2=∠3=90° ( 垂直的定义),∴BD∥EF(同位角相等,两直线平行)
∴∠4=∠5(两直线平行,同位角相等)
∵∠1=∠4( 已知)
∴∠1=∠5(等量代换)
∴DG∥BC(内错角相等,两直线平行)
∴∠ADG=∠C( 两直线平行,同位角相等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知xy<0,x<y,且|x|=1,|y|=2.
(1)求x和y的值;
(2)求
 +(xy-1)2的值.
+(xy-1)2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.

(1)在图1中以格点为顶点画一个面积为5的等腰直角三角形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、
 、
、  ;
;(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小张某天上午营运全是在东西走向的政府大道上进行的,如果规定向东为正,向西为负,他这天上午的行程是(单位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)将最后一名乘客送达目的地时,小张距上午出发点的距离是多少千米?在出发点的什么方向?
(2)若汽车耗油量为0.6升/千米,出车时,邮箱有油72.2升,若小张将最后一名乘客送达目的地,再返回出发地,问小张今天上午是否需要加油?若要加油至少需要加多少才能返回出发地?若不用加油,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.

(1)求该一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积。
-
科目: 来源: 题型:
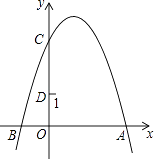
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为 .
-
科目: 来源: 题型:
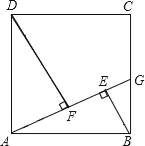
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,点G是BC边上的任意一点(不同于端点B、C),连接AG,过B、D两点作BE⊥AG,DF⊥AG,垂足分为E、F.
(1)求证:△ABE≌△DAF;
(2)若△ADF的面积为1,试求|BE﹣DF|的值.
相关试题

