【题目】如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
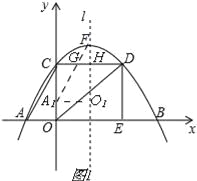
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
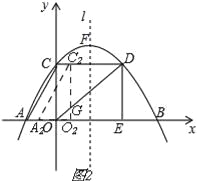
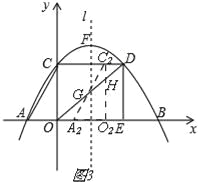
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.

参考答案:
【答案】(1)D(6,4);y=﹣![]() x2+
x2+![]() x+4;(2)
x+4;(2)![]() ;(3)当0<t≤3时,S=
;(3)当0<t≤3时,S=![]() t2,当3<t≤6时,S=
t2,当3<t≤6时,S=![]() t2﹣3t+12
t2﹣3t+12
【解析】试题分析:(1)用待定系数法求抛物线解析式;(2)由GH∥A1O1,求出GH=1,再求出FH,S重叠部分=S△A1O1F﹣S△FGH计算即可;(3)分两种情况①直接用面积公式计算,②用面积差求出即可.
试题解析:(1)∵抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).
∴设抛物线的解析式为y=a(x+3)(x﹣9), ∵C(0,4)在抛物线上, ∴4=﹣27a,
∴a=﹣![]() , ∴设抛物线的解析式为y=﹣
, ∴设抛物线的解析式为y=﹣![]() (x+3)(x﹣9)=﹣
(x+3)(x﹣9)=﹣![]() x2+
x2+![]() x+4,
x+4,
∵CD垂直于y轴,C(0,4) ∴﹣![]() x2+
x2+![]() x+4=4, ∴x=6, ∵D(6,4),
x+4=4, ∴x=6, ∵D(6,4),
(2)如图1, ∵点F是抛物线y=﹣![]() x2+
x2+![]() x+4的顶点,∴F(3,
x+4的顶点,∴F(3,![]() ), ∴FH=
), ∴FH=![]() ,
,
∵GH∥A1O1, ∴![]() , ∴
, ∴![]() , ∴GH=1,
, ∴GH=1,
∵Rt△A1O1F与矩形OCDE重叠部分是梯形A1O1HG,
∴S重叠部分=S△A1O1F﹣S△FGH=![]()
![]() A1O1×O1F﹣
A1O1×O1F﹣![]()
![]() GH×FH=
GH×FH=![]() ×3×4﹣
×3×4﹣![]() ×1×
×1×![]() =
=![]() .
.
(3)①当0<t≤3时,如图2, ∵C2O2∥DE, ∴![]() , ∴
, ∴![]() , ∴O2G=
, ∴O2G=![]() t,
t,
∴S=S△OO2G=![]() OO2×O2G=
OO2×O2G=![]() t×
t×![]() t=
t=![]() t2,
t2,
②当3<t≤6时,如图3, ∵C2H∥OC, ∴![]() , ∴
, ∴![]() , ∴C2H=
, ∴C2H=![]() (6﹣t),
(6﹣t),
∴S=S四边形A2O2HG=S△A2O2C2﹣S△C2GH=![]() OA×OC﹣
OA×OC﹣![]() C2H×(t﹣3)=
C2H×(t﹣3)=![]() ×3×4﹣
×3×4﹣![]() ×
×![]() (6﹣t)(t﹣3)=
(6﹣t)(t﹣3)=![]() t2﹣3t+12
t2﹣3t+12
∴当0<t≤3时,S=![]() t2,当3<t≤6时,S=
t2,当3<t≤6时,S=![]() t2﹣3t+12.
t2﹣3t+12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有48位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数分布直方图(横半轴表示分数,把50.5分到100.5分之间的分数分成5组,组距是10分,纵半轴表示频数)如图所示,从左到右的小矩形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )

A.9
B.18
C.12
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于y的方程ay-2=4与y-3=-1的解相同,则a的值为( )
A. 2 B. 3 C. 4 D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A.得分在70~80分之间的人数最多
B.该班的总人数为40
C.得分在90~100分之间的人数最少
D.及格(≥60分)人数是26 -
科目: 来源: 题型:
查看答案和解析>>【题目】规定新运算a*b=ab-(a+b),若(-3)*x=3,则x的值是( )
A. 0 B. 1 C. 2 D. -1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式的一次项系数是﹣5,二次项系数是8,常数项是﹣2,且只含一个字母x,请写出这个多项式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,四边彤OACB是菱形,OB在x轴的正半轴上,sin∠AOB=
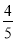 ,反比例函数
,反比例函数 在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
A. 10 B. 9 C. 8 D. 6
相关试题

