【题目】如图,在矩形ABCD中, ![]() =
= ![]() ,以点B为圆心,BC长为半径画弧,交边AD于点E.若AEED=
,以点B为圆心,BC长为半径画弧,交边AD于点E.若AEED= ![]() ,则矩形ABCD的面积为 .
,则矩形ABCD的面积为 . 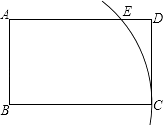
参考答案:
【答案】5
【解析】解:如图,连接BE,则BE=BC. 
设AB=3x,BC=5x,
∵四边形ABCD是矩形,
∴AB=CD=3x,AD=BC=5x,∠A=90°,
由勾股定理得:AE=4x,
则DE=5x﹣4x=x,
∵AEED= ![]() ,
,
∴4xx= ![]() ,
,
解得:x= ![]() (负数舍去),
(负数舍去),
则AB=3x= ![]() ,BC=5x=
,BC=5x= ![]() ,
,
∴矩形ABCD的面积是AB×BC= ![]() ×
× ![]() =5,
=5,
所以答案是:5.
【考点精析】本题主要考查了勾股定理的概念和矩形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
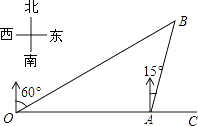
A.4km
B.2 km
km
C.2 km
km
D.( +1)km
+1)km -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB为等腰三角形,顶点A的坐标(2,
 ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A.( ,
,  )
)
B.(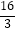 ,
,  )
)
C.( ,
,  )
)
D.(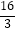 ,4
,4  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=110°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.

(1)求∠DAF的度数;
(2)如果BC=10cm,求△DAF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连接PA.设PA=x,PB=y,则(x﹣y)的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.

(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=﹣
 x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣  x+b和y=x的图象于点C、D.
x+b和y=x的图象于点C、D. 
(1)求点A的坐标;
(2)若OB=CD,求a的值.
相关试题

