【题目】如图,△ABC中,∠BAC=110°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.

(1)求∠DAF的度数;
(2)如果BC=10cm,求△DAF的周长.
参考答案:
【答案】(1)20°(2)10
【解析】试题分析:(1)先根据三角形内角和定理求出∠B+∠C,再根据等边对等角的性质可得∠BAD=∠B,∠CAF=∠C,然后代入数据进行计算即可得解;
(2)根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AD=BD,AF=CF,然后求出△ADF周长等于BC,从而得解.
试题解析:(1)∵∠BAC=110°,∴∠B+∠C=180°﹣110°=70°,
∵DE、FGQ分别是AB、AC的垂直平分线,∴AD=BD,AF=CF,∴∠BAD=∠B,∠CAF=∠C,
∴∠DAF=∠BAC﹣∠BAD﹣∠CAF=∠BAC﹣∠B﹣∠C=110°﹣70°=40°;
(2)∵DE、FGQ分别是AB、AC的垂直平分线,∴AD=BD,AF=CF,
∴△ADF周长=AD+DF+AF=BD+DF+FC=BC,
∵BC=10,∴△APQ周长=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个口袋中有红球、白球共10个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机模出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有80次摸到红球,则口袋中红球的个数大约有( )
A.8个B.7个C.3个D.2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在网络上搜索“快乐大本营“能搜索到与之相关的结果约为9480000个,将9480000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】太阳从西边升起是_____事件.(填“随机”或“必然”或“不可能”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】截止到3月26日0时,全球感染新型冠状病毒肺炎的人数已经突破380000人,“山川异域,风月同天”,携手抗“疫”,刻不容缓.将380000用科学记数法表示为( )
A.0.38×106B.3.8×106C.3.8×105D.38×104
-
科目: 来源: 题型:
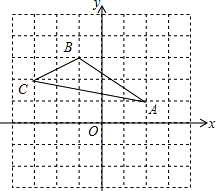
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .
相关试题

