【题目】如图,已知函数y=﹣ ![]() x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣ ![]() x+b和y=x的图象于点C、D.
x+b和y=x的图象于点C、D. 
(1)求点A的坐标;
(2)若OB=CD,求a的值.
参考答案:
【答案】
(1)解:∵点M在直线y=x的图象上,且点M的横坐标为2,
∴点M的坐标为(2,2),
把M(2,2)代入y=﹣ ![]() x+b得﹣1+b=2,解得b=3,
x+b得﹣1+b=2,解得b=3,
∴一次函数的解析式为y=﹣ ![]() x+3,
x+3,
把y=0代入y=﹣ ![]() x+3得﹣
x+3得﹣ ![]() x+3=0,解得x=6,
x+3=0,解得x=6,
∴A点坐标为(6,0);
(2)解:把x=0代入y=﹣ ![]() x+3得y=3,
x+3得y=3,
∴B点坐标为(0,3),
∵CD=OB,
∴CD=3,
∵PC⊥x轴,
∴C点坐标为(a,﹣ ![]() a+3),D点坐标为(a,a)
a+3),D点坐标为(a,a)
∴a﹣(﹣ ![]() a+3)=3,
a+3)=3,
∴a=4.
【解析】(1)先利用直线y=x上的点的坐标特征得到点M的坐标为(2,2),再把M(2,2)代入y=﹣ ![]() x+b可计算出b=3,得到一次函数的解析式为y=﹣
x+b可计算出b=3,得到一次函数的解析式为y=﹣ ![]() x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6,0);(2)先确定B点坐标为(0,3),则OB=CD=3,再表示出C点坐标为(a,﹣
x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6,0);(2)先确定B点坐标为(0,3),则OB=CD=3,再表示出C点坐标为(a,﹣ ![]() a+3),D点坐标为(a,a),所以a﹣(﹣
a+3),D点坐标为(a,a),所以a﹣(﹣ ![]() a+3)=3,然后解方程即可.
a+3)=3,然后解方程即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,
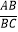 =
= 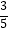 ,以点B为圆心,BC长为半径画弧,交边AD于点E.若AEED=
,以点B为圆心,BC长为半径画弧,交边AD于点E.若AEED=  ,则矩形ABCD的面积为 .
,则矩形ABCD的面积为 . 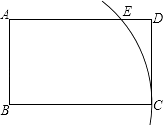
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连接PA.设PA=x,PB=y,则(x﹣y)的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.

(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=
 (x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.
(x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD. 
(1)求△OCD的面积;
(2)当BE= AC时,求CE的长.
AC时,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O上依次有A、B、C、D四个点,
 =
=  ,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF. 
(1)若⊙O的半径为3,∠DAB=120°,求劣弧 的长;
的长;
(2)求证:BF= BD;
BD;
(3)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知l1⊥l2 , ⊙O与l1 , l2都相切,⊙O的半径为2cm,矩形ABCD的边AD、AB分别与l1 , l2重合,AB=4
 cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s)
cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s)
(1)如图①,连接OA、AC,则∠OAC的度数为°;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1 , A1 , C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<2时,求t的取值范围(解答时可以利用备用图画出相关示意图).
相关试题

