【题目】无论k为何值时,直线y=k(x+3)+4都恒过平面内一个定点,这个定点的坐标为( )
A.(3,4)B.(3,﹣4)C.(﹣3,﹣4)D.(﹣3,4)
参考答案:
【答案】D
【解析】
先变式解析式得到k的不定方程x+3)k=y-4,由于k有无数个解,则x+3=0且y-4=0,然后求出x、y的值即可得到定点坐标;
解:∵y=k(x+3)+4,
∴(x+3)k=y-4,
∵无论k怎样变化,总经过一个定点,即k有无数个解,
∴x+3=0且y-4=0,
∴x=-3,y=4,
∴一次函数y=k(x+3) +4过定点(-3,4);
故选D.
-
科目: 来源: 题型:
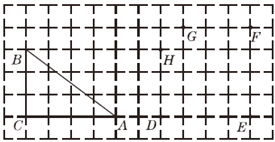
查看答案和解析>>【题目】如图所示,在方格纸中,△ABC的三个顶点及D,E,F,G,H五个点分别位于小正方形的顶点上.
(1)现以D,E,F,G,H中的三个点为顶点画三角形,在所画的三角形中与△ABC不全等但面积相等的三角形是 (只需要填一个三角形);
(2)先从D,E两个点中任意取一个点,再从F,G,H三个点中任意取两个不同的点,以所取的这三个点为顶点画三角形,画树状图求所画三角形与△ABC面积相等的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小敏将一块三角板中含45°角的顶点放在A上,从AB边开始绕点A逆时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.
(1)小敏在线段BC上取一点M,连接AM,旋转中发现:若AD平分∠BAM,则AE也平分∠MAC.请你证明小敏发现的结论;
(2)当0°<α≤45°时,小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系:BD2+CE2=DE2.同组的小颖和小亮随后想出了相同的方法进行解决:将△ABD沿AD所在的直线对折得到△ADF(如图2);请证明小敏的发现的是正确的.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.全等的两个图形成中心对称
B.成中心对称的两个图形必须重合
C.成中心对称的两个图形全等
D.旋转后能够重合的两个图形成中心对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠α=47°30′,则∠α的余角的度数为°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上有分别表示—7与2的两点A、B,若将数轴沿点B对折,使点A与数轴上的另一点C重合,则点C表示的数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=﹣2是关于x的方程3+ax=x的解,则a的值为
相关试题

