【题目】已知,在平面直角坐标系中,点A(4,0),点B(m, ![]() m),点C为线段OA上一点(点O为原点),则AB+BC的最小值为 .
m),点C为线段OA上一点(点O为原点),则AB+BC的最小值为 .
参考答案:
【答案】2 ![]()
【解析】解:∵点B(m, ![]() m),
m),
∴点B在y= ![]() x的直线上,
x的直线上,
如图,作点A关于直线OB的对称点D,过D作DC⊥OA于C交直线OB雨B,
则CD=AB+BC的最小值,
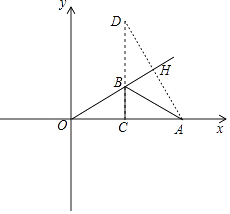
∵B(m, ![]() m),
m),
∴tan∠BOC= ![]() ,
,
∴∠AOB=30°,
∵∠AHO=90°,
∴AH= ![]() OA,
OA,
∵A(4,0),
∴OA=4,
∴AD=2AH=4,
∴DC=2 ![]() ,
,
∴AB+BC的最小值=2 ![]() ,
,
所以答案是:2 ![]() .
.
【考点精析】认真审题,首先需要了解轴对称-最短路线问题(已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径).
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l:y=mx﹣m+1(m为常数,且m≠0)与坐标轴交于A、B两点,若△AOB(O是原点)的面积恰为2,则符合要求的直线l有( )
A.1条
B.2条
C.3条
D.4条 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=°.
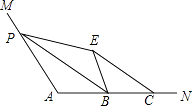
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列证明过程填空

如图,因为∠A=_____(已知),
所以AC∥ED( )
因为∠2=_____(已知),
所以AC∥ED( )
因为∠A+_____=180°(已知),
所以AB∥FD( )
因为AB∥_____(已知),
所以∠2+∠AED=180°( )
因为AC∥_____(已知),
所以∠C=∠3( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.
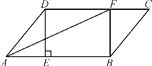
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)发现问题:如图①平行四边形AB、CD的对角线相交于点O,DE∥AC,CE∥BD,可知:四边形OCED是什么形(不需要证明).
(2)类比探究:如图②矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD,四边形OCED是什么形,请说明理由;
(3)拓展应用:如图③,菱形ABCD的对角线相交于点O,∠ABC=60°,BC=4,DE∥AC交BC的延长线于点F,CE∥BD求四边形ABFD的周长.
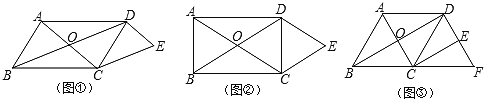
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:计算与化简
(1)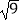 ﹣(﹣2)2+(﹣0.1)0;
﹣(﹣2)2+(﹣0.1)0;
(2)(x﹣2)2﹣(x+3)(x﹣1).
相关试题

