【题目】三角形ABC与三角形![]() 在平面直角坐标系中的位置如图所示,三角形
在平面直角坐标系中的位置如图所示,三角形![]() 是由三角形ABC经过平移得到的.
是由三角形ABC经过平移得到的.
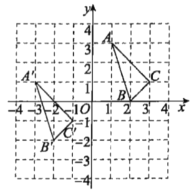
(1)分别写出点![]()
![]()
![]() 的坐标;
的坐标;
(2)说明三角形![]() 是由三角形ABC经过怎样的平移得到的;
是由三角形ABC经过怎样的平移得到的;
(3)若点![]() 是三角形ABC内的一点,则平移后点P在三角形
是三角形ABC内的一点,则平移后点P在三角形![]() 内的对应点为P‘,写出点P’的坐标.
内的对应点为P‘,写出点P’的坐标.
参考答案:
【答案】(1)![]()
![]()
![]() ;(2)三角形
;(2)三角形![]() 是由三角形ABC先向左平移4个单位长度,再向下平移2个单位长度得到的;(3)点P‘的坐标为
是由三角形ABC先向左平移4个单位长度,再向下平移2个单位长度得到的;(3)点P‘的坐标为![]()
【解析】
(1)直接根据题中的直角坐标系和图即可得出答案;
(2)找到A,B,C其中一点的平移方式,即可找到三角形的平移方式;
(3)根据点的平移规律得出答案即可.
(1)由题图知![]()
![]()
![]() ;
;
(2)三角形![]() 是由三角形ABC先向左平移4个单位长度,再向下平移2个单位长度得到的;
是由三角形ABC先向左平移4个单位长度,再向下平移2个单位长度得到的;
(3)点P‘的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线
 ,
, 分别交
分别交 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求
 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组乘一辆汽车沿公路检修线路,约定向东走为正,向西走为负。某天从A地出发到收工时,行走记录(长度单位:千米)为:+15,-2,+5,-1,+10,-3。
⑴问收工时,检修小组在A处的哪一边,距A地多远?
⑵若汽车每千米的耗油为
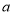 升,求从出发到收工共耗油多少升?
升,求从出发到收工共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
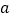 正方形OABC的边OA、OC在坐标轴上.在
正方形OABC的边OA、OC在坐标轴上.在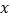 轴上线段
轴上线段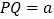 (Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为
(Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为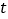 .连接PB,过P作PB的垂线,过Q作
.连接PB,过P作PB的垂线,过Q作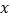 轴的垂线,两垂线相交于点D.连接BD交
轴的垂线,两垂线相交于点D.连接BD交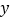 轴于点E,连接PD交
轴于点E,连接PD交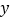 轴于点F,连接PE.
轴于点F,连接PE.(1)求∠PBD的度数.
(2)设△POE的周长为
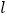 ,探索
,探索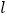 与
与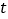 的函数关系式,并写出
的函数关系式,并写出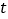 的取值范围.
的取值范围.(3)令
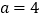 ,当△PBE为等腰三角形时,求△EFD的面积.
,当△PBE为等腰三角形时,求△EFD的面积.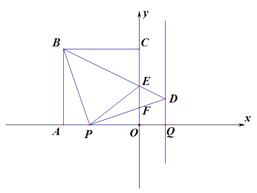
-
科目: 来源: 题型:
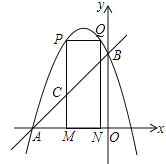
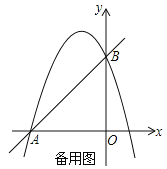
查看答案和解析>>【题目】如图,直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P为抛物线在第二象限内一点,过点P作x轴的垂线,垂足为点M,与直线AB交于点C,过点P作x轴的平行线交抛物线于点Q,过点Q作x轴的垂线,垂足为点N,若点P在点Q左边,设点P的横坐标为m.
①当矩形PQNM的周长最大时,求△ACM的面积;
②在①的条件下,当矩形PMNQ的周长最大时,G是直线AC上一点,F是抛物线上一点,是否存在点G,使得以点P、C、G、F为顶点的四边形是平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.
相关试题

