Question

【题目】如图，已知∠ABC=90°, D是直线AB上的点，AD=BC ，过点A作AF⊥AB,并截取AF=DB ,连接DC、DF、CF ，判断△CDF的形状并证明.

Answer 1

【答案】△是等腰直角三角形，证明见解析

【解析】

试题由“ASA”证明△ADF≌△BCD得到DF=CD，∠ADF=∠BCD，再利用∠BCD+∠CDB=90°得到∠CDF=90°，则可判断△CDF为等腰直角三角形.

试题解析：△是等腰直角三角形，

证明如下：

∵AF⊥AD，∠ABC=90°，

∴∠FAD=∠DBC，

在△FAD与△DBC中，

，

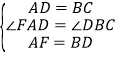∴△FAD≌△DBC（SAS）；

∴FD=DC，

∴△CDF是等腰三角形，

∵△FAD≌△DBC，

∴∠FDA=∠DCB，

∵∠BDC+∠DCB=90°，

∴∠BDC+∠FDA=90°，

∴△CDF是等腰直角三角形.