【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() ,垂足
,垂足![]() 在线段
在线段![]() 上,连接
上,连接![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,则
,则![]() °.
°.
参考答案:
【答案】(1)见解析;(2)105.
【解析】
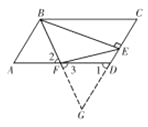
(1)分别延长![]() ,
,![]() 交于点
交于点![]() ,先证明
,先证明![]() 得BF=FG,再证明
得BF=FG,再证明![]() 为
为![]() 的中线即可得到结论;
的中线即可得到结论;
(2)设∠FEB=x,则∠FBE=x,求得∠EFB=180°-2x,∠AFB=90°-x,证明∠AFE=3∠DEF即可求得结论.
(1) 证明:如图,分别延长![]() ,
,![]() 交于点
交于点![]() ,
,
∵四边形![]() 是平行四边形.
是平行四边形.
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
在![]() 与
与![]() 中,
中,
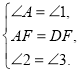
∴![]()
∴![]() .
.
即![]() 为
为![]() 的中线.
的中线.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
(2) ∵![]()
∴∠FEB=∠FBE
设∠FEB=x,则∠FBE=x,
∵AB//CD, BE⊥CD
∴∠ABE=90゜
∴∠ABF=∠AFB=90°-x,
∴∠EFB=180°-2x,
∴∠EFA=90°-x+180°-2x=270°-3x,
∵∠DEF=90°-x,且![]()
∴∠AFE=3∠DEF=105°.
故答案为:105°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其它均相同)打乱顺序重新排列,从中任意抽取1张卡片.
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率;
(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由;
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的. -
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1 000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟.其中正确的说法是_________________(把你认为正确说法的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个直角三角形纸片
 放置在平面直角坐标系中,
放置在平面直角坐标系中, 是坐标原点,点
是坐标原点,点 坐标为
坐标为 ,点
,点 坐标为
坐标为 ,
, ,点
,点 是边
是边 上一点(点
上一点(点 不与点
不与点 ,点
,点 重合),沿
重合),沿 折叠该纸片,点
折叠该纸片,点 的对应点为点
的对应点为点 ,连接
,连接 .
.
(1)如图1,当点
 在第一象限,且
在第一象限,且 时,求点
时,求点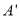 的坐标;
的坐标;(2)如图2,当点
 为
为 的中点时;
的中点时;①求证:
 ;
;②直接写出四边形
 的面积;
的面积;(3)当
 时,直接写出点
时,直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 发现:
如图1,点
 是线段
是线段 外一动点,且
外一动点,且 ,
, .当点
.当点 位于 时,线段
位于 时,线段 的长取得最大值;最大值为 (用含
的长取得最大值;最大值为 (用含 ,
, 的式子表示).
的式子表示).
(2)应用:
如图2,点
 为线段
为线段 外一动点,
外一动点, ,
, ,分别以
,分别以 ,
, 为边在
为边在 外部作等边
外部作等边 和等边
和等边 ,连接
,连接 ,
, .
.①求证:
 ;
;②直接写出线段
 长的最大值.
长的最大值.(3)拓展:
如图3,在平面直角坐标系中,点
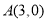 ,点
,点 ,点
,点 为线段
为线段 外一动点,
外一动点, ,
, ,
, ,请直接写出线段
,请直接写出线段 长的最大值及此时点
长的最大值及此时点 的坐标.
的坐标.
相关试题

