【题目】暖羊羊有5张写着不同数字的卡片,请你按要求选择卡片,完成下列各问题:
![]()
(1)从中选择两张卡片,使这两张卡片上数字的乘积最大.
这两张卡片上的数字分别是 ,积为 _.
(2)从中选择两张卡片,使这两张卡片上数字相除的商最小.
这两张卡片上的数字分别是 ,商为 .
(3)从中选择4张卡片,每张卡片上的数字只能用一次,选择加、减、乘、除中的适当方法(可加括号),使其运算结果为24,写出运算式子.(写出一种即可)
参考答案:
【答案】(1)-5和-3,15 ; (2) -5和+3, ![]() ; (3)
; (3)![]() (答案不唯一)
(答案不唯一)
【解析】
(1)要想乘积最大,必须积为正数才有最大值,也就是必须选择同号的两个数相乘,然后取积最大的两个卡片即可.
(2)要想商最小,必须商为负数才最小值,也就是必须选择异号的两个数相除且被除数的绝对值要大于除数的绝对值,然后选择商最小的两个卡片即可.
(3)把24分解因数,可得到2×12=24,3×8=24,4×6=24,然后找到合适的卡片能够通过运算得到24的因数即可.
(1)要想乘积最大,必须积为正数才有最大值,选择同号的两个数相乘
则有(+3)×(+4)=12,(-5)×(-3)=15
积最大为15,所以选择卡片-5和卡片-3
(2) 要想商最小,必须商为负数才最小值,选择异号的两个数相除且被除数的绝对值要大于除数的绝对值.
则有(-5)÷3=![]() ,(-5)÷4=
,(-5)÷4=![]() ,4÷(-3)=
,4÷(-3)=![]()
商最小为![]() ,所选择卡片-5和卡片+3
,所选择卡片-5和卡片+3
(3) 把24分解因数,可得到2×12=24,3×8=24,4×6=24等形式.
当2×12=24时,2=(-3)-(-5),12=3×4
则[(-3)-(-5)]×3×4=12
故选择卡片数字为:-3,-5,+3,+4
当3×8=24时,可得-3×(-8)=24,则-8=(-5)-3
则-3×[(-5)-3]=24.
同理可继续推导.
故答案为:(1)-5和-3,15 ;(2) -5和+3![]() ;(3)
;(3)![]() (答案不唯一)
(答案不唯一)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在普通商场中用96元购买了一种商品,后来他在网上发现完全相同的这一商品在网上购买比普通商场中每件少2元,他用90元在网上再次购买这一商品,比上次在普通商场中多买了3件.问小明在网上购买的这一商品每件几元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.

(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象如图,有以下结论:
的图象如图,有以下结论:①m<0;
②在每一个分支上,y随x的增大而增大;
③若点A(-1,a)、B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(-x,-y)也在图象上.
其中正确结论的个数为( )

A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
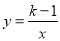 (k为常数,k≠1).
(k为常数,k≠1).(1)其图象与正比例函数y=x的图象的一个交点为P.若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(3)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1),B(x2,y2),当y1>y2时,试比较x1与x2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小华是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公交汽车到了学校.如图是他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图.则下列说法中错误的是( )
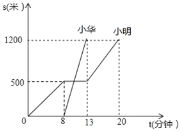
A.小明吃早餐用时5分钟
B.小华到学校的平均速度是240米/分
C.小明跑步的平均速度是100米/分
D.小华到学校的时间是7:55
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习了“乘方”运算,下面介绍一种新运算,即“对数”运算.
定义:如果
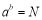 (a>0,a≠1,N>0),那么b叫做以a为底N的对数,记作
(a>0,a≠1,N>0),那么b叫做以a为底N的对数,记作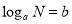 .
.例如:因为
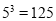 ,所以
,所以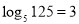 ;因为
;因为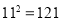 ,所以
,所以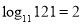 .
.根据“对数”运算的定义,回答下列问题:
(1)填空:
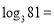 ,
,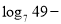
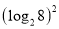 = .
= .(2)已知m,n为整数,且|m-2|+|m-n|=
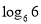 ,求m+n的值.
,求m+n的值.(3) 对于“对数”运算,小明同学认为有“
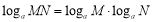 (a>0,a≠1,M>0,N>0)”,他的说法正确吗?如果正确,请说明理由;如果不正确,请举出一个反例加以说明,并写出正确的结论.
(a>0,a≠1,M>0,N>0)”,他的说法正确吗?如果正确,请说明理由;如果不正确,请举出一个反例加以说明,并写出正确的结论.
相关试题

