【题目】如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.

(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
参考答案:
【答案】(1)C(0,6)。
(2)y=![]() x+6。
x+6。
(3)P1(4,3),P2(![]() )P3(
)P3(![]() ),P4(
),P4(![]() )。
)。
【解析】
试题
(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;
(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.
试题解析:
(1)解方程x2-14x+48=0得
x1=6,x2=8
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根
∴OC=6,OA=8
∴C(0,6)
(2)设直线MN的解析式是y=kx+b(k≠0)
由(1)知,OA=8,则A(8,0)
∵点A、C都在直线MN上
∴![]()
解得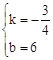 ,
,
∴直线MN的解析式为y=-![]() x+6
x+6
(3)
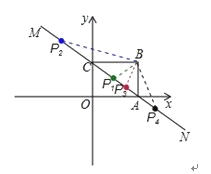
∵A(8,0),C(0,6)
∴根据题意知B(8,6)
∵点P在直线MN y=-![]() x+6上
x+6上
∴设P(a,--![]() a+6)
a+6)
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(-![]() a+6-6)2=64
a+6-6)2=64
解得,a=±![]() ,则P2(-
,则P2(-![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )
)
③当PB=BC时,(a-8)2+(-![]() a+6-6)2=64
a+6-6)2=64
解得,a=![]() ,则-
,则-![]() a+6=-
a+6=-![]()
∴P4(![]() ,
,![]() )
)
综上所述,符合条件的点P有:P1(4,3),P2(-![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ),P4(
),P4(![]() ,-
,-![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B所表示的数分别为a和b,且满足|a+3|+(b-9)2018=0,O为原点
(1) 试求a和b的值
(2) 点C从O点出发向右运动,经过3秒后点C到A点的距离是点C到B点距离的3倍,求点C的运动速度?
(3) 点D以1个单位每秒的速度从点O向右运动,同时点P从点A出发以5个单位每秒的速度向左运动,点Q从点B出发,以20个单位每秒的速度向右运动.在运动过程中,M、N分别为PD、OQ的中点,问
 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按如图所示方式搭图形,按照这种方式搭下去,搭第9个图形需火柴棒的根数是( )

A. 48 B. 54 C. 60 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】点E在正方形ABCD外,BE=4,CE=2,∠BEC=135°,将△BEC绕点B逆时针旋转得到△BFA,求FE,FC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2x2+3xy﹣2x﹣1,B=﹣x2+xy﹣1:
(1)求3A+6B;
(2)若3A+6B的值与x无关,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣
 x2+bx﹣6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
x2+bx﹣6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA,BC,求△ABC的面积. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
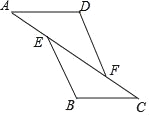
A. ∠D=∠B B. AD=CB C. BE=DF D. ∠AFD=∠CEB
相关试题

