【题目】为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如图的调查问卷(单选).在随机调查了某市全部5 000名司机中的部分司机后,统计整理并制作了如下的统计图: 

根据以上信息解答下列问题:
(1)补全条形统计图 , 并计算扇形统计图中m=;
(2)该市支持选项B的司机大约有多少人?
(3)若要从该市支持选项B的司机中随机选择100名,给他们发放“请勿酒驾”的提醒标志,则支持该选项的司机小李被选中的概率是多少?
参考答案:
【答案】
(1) ;20
;20
(2)解:支持选项B的人数大约为:5000×23%=1150.
答:该市支持选项B的司机大约有1150人
(3)解:∵总人数=5000×23%=1150人,
∴小李被选中的概率是: ![]() =
= ![]() .
.
答:支持该选项的司机小李被选中的概率是 ![]()
【解析】解:(1)69÷23%﹣60﹣69﹣36﹣45=90(人). C选项的频数为90,m%=60÷(69÷23%)=20%.
所以m=20;
故答案为:20;
(1)先算出C组里的人数,根据条形图B的人数,和扇形图B所占的百分比求出总人数,然后减去其他4组的人数,求出C的人数.(2)全市所以司机的人数×支持选项B的人数的百分比可求出结果.(3)根据(2)算出的支持B的人数,以及随机选择100名,给他们发放“请勿酒驾”的提醒标志,则可算出支持该选项的司机小李被选中的概率是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个几何体的三视图,根据图示的数据可计算出该几何体的表面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,BC=2AD=2
 ,点E是BC边的中点,△DEF是等边三角形,DF交AB于点G,则△BFG的周长为 .
,点E是BC边的中点,△DEF是等边三角形,DF交AB于点G,则△BFG的周长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.
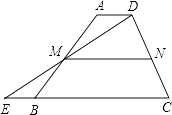
(1)求证:△AMD≌△BME;
(2)若N是CD的中点,且MN=5,BE=2,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,I点为△ABC的内心,D点在BC上,且ID⊥BC,若∠B=44°,∠C=56°,则∠AID的度数为何?( )

A. 174 B. 176 C. 178 D. 180
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在计算一个多边形(每个内角小于180°)的内角和时,由于粗心少算了一个内角,
结果得到的总和是2018°,则少算了这个内角的度数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,中原福塔(河南广播电视塔)是世界第﹣高钢塔.小明所在的课外活动小组在距地面268米高的室外观光层的点D处,测得地面上点B的俯角α为45°,点D到AO的距离DG为10米;从地面上的点B沿BO方向走50米到达点C处,测得塔尖A的仰角β为60°.请你根据以上数据计算塔高AO,并求出计算结果与实际塔高388米之间的误差.(参考数据:
 ≈1.732,
≈1.732,  ≈1.414.结果精确到0.1米)
≈1.414.结果精确到0.1米)
相关试题

