【题目】点A、B、C在数轴上表示的数a、b、c满足(b+3)2+|c﹣24|=0,且多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式.
(1)分别求a、b、c的值;
(2)已知点P、点Q是数轴上的两个动点,点P从点A出发,以3个单位/秒的速度向右运动,同时点Q从点C出发,以7个单位/秒的速度向左运动:
①若点P和点Q经过t秒后在数轴上的点D处相遇,求出t的值和点D所表示的数;
②若点P运动到点B处,动点Q再出发,则P运动几秒后这两点之间的距离为5个单位?
参考答案:
【答案】
(1)解:∵(b+3)2+|c﹣24|=0,
∴b=﹣3,c=24,
∵多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式,
∴|a+3|=5﹣2,﹣a≠0,
∴a=﹣6.
故答案是:﹣6;﹣3;24
(2)解:①依题意得 3t+7t=|﹣6﹣24|=30,
解得 t=3,
则3t=9,
所以﹣6+9=3,
所以出t的值是3和点D所表示的数是3.
②设点P运动x秒后,P、Q两点间的距离是5.
当点P在点Q的左边时,3x+5+7(x﹣1)=30,
解得 x=3.2.
当点P在点Q的右边时,3x﹣5+7(x﹣1)=30,
解得 x=4.2.
综上所述,当点P运动3.2秒或4.2秒后,这两点之间的距离为5个单位.
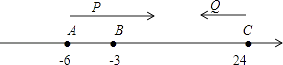
【解析】(1)利用非负数的性质求出b与c的值,根据多项式为五次四项式求出a的值;(2)①利用点P、Q所走的路程=AC列出方程;②此题需要分类讨论:相遇前和相遇后两种情况下PQ=5所需要的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.A、B、C三点在数轴上,A表示的数为-10,B表示的数为14,点C在点A与点B之间,且AC=BC.
(1)求A、B两点间的距离;
(2)求C点对应的数;
(3)甲、乙分别从A、B两点同时相向运动,甲的速度是1个单位长度/s,乙的速度是2个单位长度/s,求相遇点D对应的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场把一个双肩背包按进价提高50%标价,然后再按八折出售,这样商场每卖出一个书包就可盈利8元,求每个双肩背书包的进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为
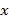 (小时),两车之间的距离为
(小时),两车之间的距离为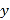 (千米),如图中的折线表示
(千米),如图中的折线表示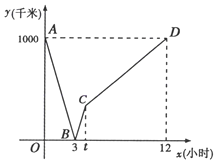 与
与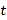 之间的函数关系.
之间的函数关系.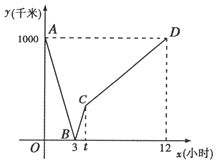
根据图象进行以下探究:
(1)西宁到西安两地相距_________千米,两车出发后___________小时相遇;
普通列车到达终点共需__________小时,普通列车的速度是___________千米/小时.
(2)求动车的速度;
(3)普通列车行驶
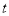 小时后,动车的达终点西宁,求此时普通列车还需行驶多少千米到达西安?
小时后,动车的达终点西宁,求此时普通列车还需行驶多少千米到达西安? -
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.
(1)请你用画树状图或列表法求出甲、乙二人在同一层楼出电梯的概率;
(2)小亮和小芳打赌说:“若甲、乙在同一层或相邻楼层出电梯,则小亮胜,否则小芳胜”.该游戏是否公平?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学进行绿地改造,原有一正方形绿地,现将它每边都增加3m,则面积增加了63m2 . 问:原绿地的边长为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:[(x+2y)(x﹣2y)﹣(x+4y)2]÷4y,其中x=1,y=4.
相关试题

