【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D,E,求AD的长. 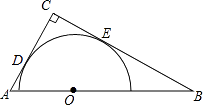
参考答案:
【答案】解:连接OD、OE,设AD=x, 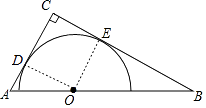
∵半圆分别与AC、BC相切于点D、E,
∴∠CDO=∠CEO=90°,CD=CE,
又∵∠C=90°,
∴四边形ODCE是正方形,
∴OD∥BC,
∴△AOD∽△ABC,
∴ ![]() ,
,
又∵AC=4,
∴OD=CD=4﹣x,
又∵BC=6,
∴ ![]() =
= ![]() ,
,
解得:x=1.6,
∴AD=1.6.
【解析】连接OD、OE,设AD=x,根据正方形的判定求出四边形ODCE是正方形,推出OD∥BC,根据相似三角形的判定得出△AOD∽△ABC,得出比例式,代入即可求出答案.
【考点精析】掌握切线的性质定理和相似三角形的判定与性质是解答本题的根本,需要知道切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是( )

A.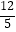
B.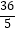
C.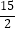
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,其对称轴方程为x=﹣1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0,则正确的结论是( )
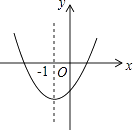
A.①②③④
B.②④⑤
C.①④⑤
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为(结果保留π)
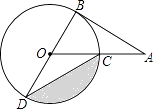
-
科目: 来源: 题型:
查看答案和解析>>【题目】为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.请根据图表中提供的信息,解答下列问题:
整理情况
频数
频率
非常好
0.21
较好
70
一般
不好
36
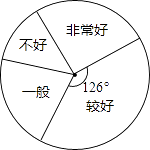
(1)本次抽样共调查了多少学生?
(2)补全统计表中所缺的数据.
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66.5°.
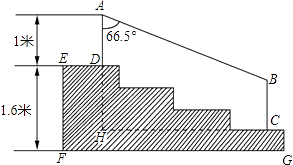
(1)求点D与点C的高度差DH;
(2)求所用不锈钢材料的总长度l.(即AD+AB+BC,结果精确到0.1米) (参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
相关试题

