【题目】已知:如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC与点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.下列结论:①CD2=CE·CB;②4EF 2=ED ·EA;③∠OCB=∠EAB;④![]() .其中正确的只有____________________.(填序号)
.其中正确的只有____________________.(填序号)

参考答案:
【答案】①、②、④
【解析】试题分析:先连接BD,利用相似三角形的判定以及切线的性质定理得出DF=FB,进而分别得出△CDE∽△CBD以及△CDF∽△CBO,再根据相似三角形的性质分别分析即可得出答案.
①连接BD,∵AB为直径,∴∠ADB=90°,∴∠DBE+∠3=90°,∵∠ABC=90°,
∴∠1+∠DBE=90°,∴∠1=∠3,又∵DO=BO,∴∠1=∠2,∴∠2=∠3,
∴∠CDB=∠CED,∵∠DCB=∠ECD,∴△CDE∽△CBD,∴![]() ,故①正确;
,故①正确;
②∵过D作⊙O的切线交BC于点F,∴FD是⊙O的切线,∵∠ABC=90°,
∴CB是⊙O的切线,∴FB=DF,∴∠FDB=∠FBD,∴∠1=∠FDE,∴∠FDE=∠3,
∴DF=EF,∴EF=FB,∴EB=2EF,∵在Rt△ABE中,BD⊥AE,∴![]() ,
,
∴![]() ,故②正确;
,故②正确;
③∵AO=DO,∴∠OAD=∠ADO,假设③∠OCB=∠EAB成立,则∠OCB=0.5∠COB,
∴∠OCB=30°,而![]() ,与tan30°=
,与tan30°= ![]() 矛盾,
矛盾,
故③∠OCB=∠EAB不成立,故此选项错误;
④∵∠CDF=∠CBO=90°,∠DCF=∠OCB,∴△CDF∽△CBO,∴![]() ,∴
,∴![]() ,
,
∵AB=BC,∴DF=0.5CD;故④正确.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F.
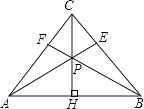
(1)证明:∠CAE=∠CBF;
(2)证明:AE=BF. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,ABCD中,E、F分别是边AB、CD的中点.

(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB两端点的坐标分别为A(2,4),B(5,2),若将线段AB平移,使得点B的对应点为点C(3,﹣1).则平移后点A的对应点的坐标为
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P到x轴的距离是2,到y轴的距离是3,且点P在y轴的右侧,则P点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=
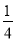 ,求BN的长.
,求BN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(3,一1)的位置在( )
A.第一象限B.第二象限C.第三象限D.第四象限
相关试题

