Question

【题目】如图，在等腰△ABC中，CH是底边上的高线，点P是线段CH上不与端点重合的任意一点，连接AP交BC于点E，连接BP交AC于点F．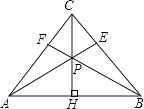
（1）证明：∠CAE=∠CBF；
（2）证明：AE=BF．

Answer 1

【答案】
（1）证明：在等腰△ABC中，

∵CH是底边上的高线，

∴∠ACH=∠BCH，

在△ACP和△BCP中， ，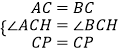

∴△ACP≌△BCP（SAS），

∴∠CAE=∠CBF（全等三角形对应角相等）

（2）在△AEC和△BFC中 ，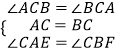

∴△AEC≌△BFC（ASA），

∴AE=BF（全等三角形对应边相等）．

【解析】（1）根据等腰三角形三线合一的性质可得CH平分∠ACB，再证明△ACE和△BCF全等，然后根据全等三角形对应角相等可得结论；（2）证明△AEC≌△BFC，根据全等三角形对应边相等即可证明．
【考点精析】本题主要考查了等腰三角形的性质的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）才能正确解答此题．