【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九“勾股”章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”译文:“如图,今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)你的计算结果是:出南门________步而见木.

参考答案:
【答案】315
【解析】
根据题意写出AB、AC、CD的长,根据相似三角形的性质得到比例式,计算即可.
由题意得,AB=15里,AC=4.5里,CD=3.5里,
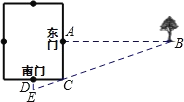
△ACB∽△DEC,
∴![]() ,即
,即![]()
解得,DE=1.05里=315步,
∴走出南门315步恰好能望见这棵树,
故答案为:315.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).

(1)仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.
(2)如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
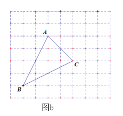
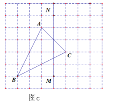
(3)如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图a,P、Q是△ABC的边BC上的两点,且△APQ为等边三角形,AB=AC,
(1)求证:BP=CQ.
(2)如图a,若∠BAC=120
 ,AP=3,求BC的长.
,AP=3,求BC的长.(3)若∠BAC=120
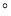 ,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.
,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.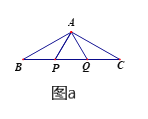

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,E,D是BC边的三等分点,F是AC的中点,BF分别交AD,AE于点G,H,则BG∶GH∶HF等于( )
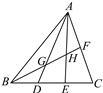
A. 1∶2∶3 B. 3∶5∶2 C. 5∶3∶2 D. 5∶3∶1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD∽四边形A′B′C′D′,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)
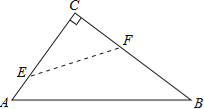
(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为 ;
②当AC=3,BC=4时,AD的长为 ;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
相关试题

