【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)
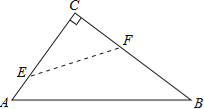
(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为 ;
②当AC=3,BC=4时,AD的长为 ;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
参考答案:
【答案】解:(1)①![]() 。
。
②![]() 或
或![]() 。
。
(2)当点D是AB的中点时,△CEF与△ABC相似。理由如下:
如答图3所示,连接CD,与EF交于点Q,
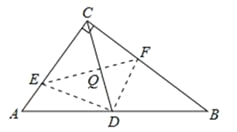
∵CD是Rt△ABC的中线,∴CD=DB=AB,∴∠DCB=∠B。
由折叠性质可知,∠CQF=∠DQF=90°,
∴∠DCB+∠CFE=90°。
∵∠B+∠A=90°,∴∠CFE=∠A。
又∵∠C=∠C,∴△CEF∽△CBA。
【解析】
(1)若△CEF与△ABC相似.
①当AC=BC=2时,△ABC为等腰直角三角形,如答图1所示,
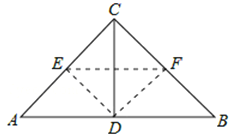
此时D为AB边中点,AD=![]() AC=
AC=![]() 。
。
②当AC=3,BC=4时,有两种情况:
(I)若CE:CF=3:4,如答图2所示,
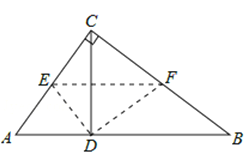
∵CE:CF=AC:BC,∴EF∥BC。
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高。
在Rt△ABC中,AC=3,BC=4,∴BC=5。
∴cosA=![]() 。∴AD=ACcosA=3×
。∴AD=ACcosA=3×![]() =
=![]() 。
。
(II)若CF:CE=3:4,如答图3所示.
∵△CEF∽△CAB,∴∠CEF=∠B。
由折叠性质可知,∠CEF+∠ECD=90°。
又∵∠A+∠B=90°,∴∠A=∠ECD,∴AD=CD。
同理可得:∠B=∠FCD,CD=BD。∴AD=BD。
∴此时AD=AB=![]() ×5=
×5=![]() .
.
综上所述,当AC=3,BC=4时,AD的长为![]() 或
或![]() 。
。
(2)当点D是AB的中点时,△CEF与△ABC相似.可以推出∠CFE=∠A,∠C=∠C,从而可以证明两个三角形相似。
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九“勾股”章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”译文:“如图,今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)你的计算结果是:出南门________步而见木.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD∽四边形A′B′C′D′,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
(1)“快车”行驶里程不超过5公里计费8元;
(2)“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
(3)A点的坐标为(6.5,10.4);
(4)从哈尔滨西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+k﹣2经过点(m,n+1)和(m+1,2n+3),且﹣2<k<0,则n的取值范围是( )
A. ﹣2<n<0B. ﹣4<n<﹣2C. ﹣4<n<0D. 0<n<﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)操作发现如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决(设DF=x,AD=y.)
保持(1)中的条件不变,若DC=2DF,求
 的值;
的值;(3)类比探求
保持(1)中条件不变,若DC=nDF,求
 的值.
的值.
相关试题

