【题目】如图,在△ABC中,E,D是BC边的三等分点,F是AC的中点,BF分别交AD,AE于点G,H,则BG∶GH∶HF等于( )
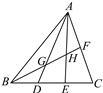
A. 1∶2∶3 B. 3∶5∶2 C. 5∶3∶2 D. 5∶3∶1
参考答案:
【答案】C
【解析】
作FM∥BC交AE于点M,则根据△BEH∽△FMH,利用BF表示出HF的长度,作DN∥AC交BF于点N,则△BDN∽△BCF且△DNG∽△AFG,依据△BDN∽△BCF可以用BF表示出BN的长,然后依据△DNG∽△AFG表示出NG的长,则BG,GM,HF都可以利用BF表示出来,则比值即可求解.
设BC=6a,则BD=DE=EC=2a,作FM∥BC交AE于点M,

∵F是AC的中点,
∴![]()
∵FM∥BC,
∴△BEH∽△FMH,
∴![]() 则
则![]()
作DN∥AC交BF于点N,设AC=2b,则AF=CF=b,
∴△BDN∽△BCF,
∴![]()
∴![]()
∵DN∥AC,
∴△DNG∽△AFG,
∴![]()
∴![]() ,即
,即![]()
∴![]()
∴![]()
∴![]()
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
-
科目: 来源: 题型:
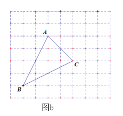
查看答案和解析>>【题目】如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).

(1)仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.
(2)如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
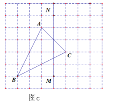
(3)如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图a,P、Q是△ABC的边BC上的两点,且△APQ为等边三角形,AB=AC,
(1)求证:BP=CQ.
(2)如图a,若∠BAC=120
 ,AP=3,求BC的长.
,AP=3,求BC的长.(3)若∠BAC=120
 ,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.
,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.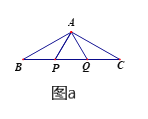

-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九“勾股”章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”译文:“如图,今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)你的计算结果是:出南门________步而见木.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD∽四边形A′B′C′D′,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

相关试题

