【题目】△ABC中,∠C=90°,AB=13,AC=12,以B为圆心,5为半径的圆与直线AC的位置关系是( )
A. 相切B. 相交C. 相离D. 不能确定
参考答案:
【答案】A
【解析】
此题首先应求得圆心到直线的距离,即是直角三角形直角边BC的长;再根据直线和圆的位置关系与数量之间的联系进行判断.
若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解:∵在△ABC中,∠C=90°,AB=13,AC=12,
∴根据勾股定理求得直角边BC是5;
则圆心到直线的距离是5,
∵⊙B的半径是5,
∴以B为圆心,5为半径的圆与直线AC的位置关系是相切.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的集合里
+6,﹣8,﹣0.4,0,230%, ,﹣1
,﹣1 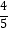 ,﹣(﹣5),﹣|﹣2|,﹣
,﹣(﹣5),﹣|﹣2|,﹣  ,0.010010001…,﹣2.33…
,0.010010001…,﹣2.33…
(1)正数集合:{};
(2)负数集合:{ };
(3)整数集合:{};
(4)无理数集合:{}. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知|x﹣5|+(2y+6)2=0,A=﹣x2﹣2xy+y2 , B=﹣
 x2﹣6xy+3y2 .
x2﹣6xy+3y2 .
(1)求y﹣x的值.
(2)求3A﹣[2A﹣B﹣4(A﹣B)]的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果多项式x2-kx+9可直接用公式法因式分解,那么k的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图)
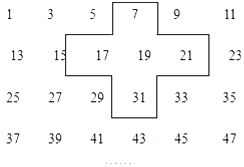
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2015吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】过圆外一点可以作圆的______条切线;过圆上一点可以作圆的_____条切线;过圆内一点的圆的切线______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解
(1)3a2﹣12;
(2)x3y﹣2x2y2+xy3;
(3)(x+1)(x+3)+1.
相关试题

