【题目】如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C,楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度(结果精确到0.1m).(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
参考答案:
【答案】解:过点D作DE⊥AB于点E,得矩形DEBC,
设塔高AB=xm,则AE=(x﹣10)m,
在Rt△ADE中,∠ADE=30°,
则DE= ![]() (x﹣10)米,
(x﹣10)米,
在Rt△ABC中,∠ACB=45°,
则BC=AB=x,
由题意得, ![]() (x﹣10)=x,
(x﹣10)=x,
解得:x=15+5 ![]() ≈23.7.即AB≈23.7米.
≈23.7.即AB≈23.7米.
答:塔的高度约为23.7米.
【解析】过点D作DE⊥AB于点E,设塔高AB=x,则AE=(x﹣10)m,在Rt△ADE中表示出DE,在Rt△ABC中表示出BC,再由DE=BC可建立方程,解出即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图
 ).图
).图 是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形
是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形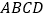 、正方形
、正方形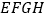 、正方形
、正方形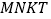 的面积分别为
的面积分别为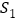 、
、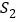 、
、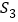 .若
.若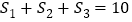 ,则
,则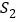 的值是( )
的值是( )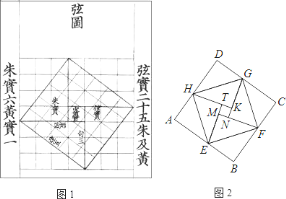
A.
 B.
B. 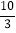 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
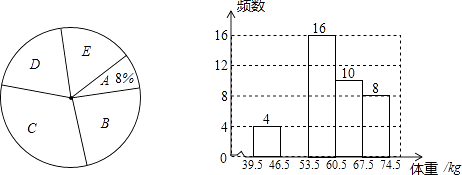
解答下列问题:
(1)这次抽样调查的样本容量是 , 并补全频数分布直方图;
(2)C组学生的频率为 , 在扇形统计图中D组的圆心角是度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
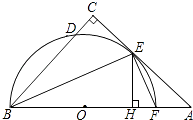
(1)求证:AC是⊙O的切线.
(2)过点E作EH⊥AB于点H,求证:CD=HF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.
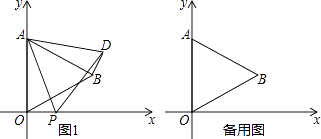
(1)求B的坐标;
(2)当点P运动到点(t,0)时,试用含t的式子表示点D的坐标;
(3)是否存在点P,使△OPD的面积等于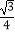 ,若存在,请求出符合条件的点P的坐标(直接写出结果即可)
,若存在,请求出符合条件的点P的坐标(直接写出结果即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),
 ,
, ,从三角板的刻度可知
,从三角板的刻度可知 ,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________
,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与直线y=
 x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,
x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,  ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.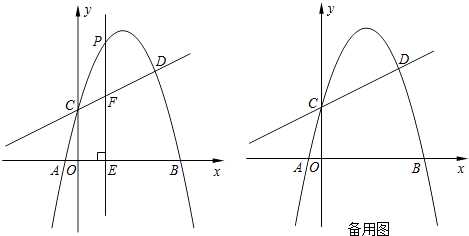
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.
相关试题

