【题目】如图,已知AB∥CD,点M,N分别是AB,CD上两点,点G在AB,CD之间.
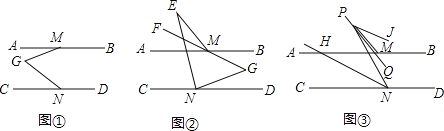
(1)求证:∠AMG+∠CNG=∠MGN;
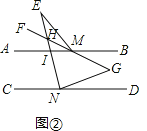
(2)如图②,点E是AB上方一点,MF平分∠AME,若点G恰好在MF的反向延长线上,且NE平分∠CNG,2∠E+∠G=90°,求∠AME的度数;
(3)如图③,若点P是(2)中的EM上一动点,PQ平分∠MPQ.NH平分∠PNC,交AB于点H,PJ∥NH,直接写出∠JPQ的度数.
参考答案:
【答案】(1)见解析;(2)∠AME=60°;(3)∠JPQ=30°.
【解析】
(1)过点G作GE∥AB,得出AB∥CD∥GE,再由平行线的性质即可得出结论;
(2)设FG与NE交点为H点,AB与NE的交点I,由三角形内角和定理可知∠G+∠HNG+∠NHG=180°,再利用角平分线定理得出即90°+![]() ∠AME=180°,继而得出结论;
∠AME=180°,继而得出结论;
(3)根据PQ平分∠MPN,NH平分∠PNC,可得出∠JPQ=∠JPN﹣![]() ∠MPN,由此得出结论.
∠MPN,由此得出结论.
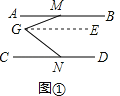
解:(1)证明:如图①,过点G作GE∥AB,
∵AB∥CD,
∴AB∥CD∥GE,
∴∠AMG=∠MGE,∠CNG=∠NGE,
∴∠AMG+∠CNG=∠MGN;
(2)如图②,设FG与NE交点为H点,AB与NE的交点I,
在△HNG中,
∵∠G+∠HNG+∠NHG=180°
∴∠HNG=∠AIE=∠IHM+∠IMH=(∠E+∠EMF)+∠IMH=∠E+(∠EMF+∠IMH )=∠E+∠AME
∠NHG=∠IHM=∠E+∠EMF=∠E+![]() ∠AME
∠AME
∴∠G+∠HNG+∠NHG=∠G+(∠E+∠AME)+(∠E+![]() ∠AME)=180° (∠G+2∠E)+
∠AME)=180° (∠G+2∠E)+![]() ∠AME=180°,即90°+
∠AME=180°,即90°+![]() ∠AME=180°,
∠AME=180°,
∴∠AME=60°;
(3)∵PQ平分∠MPN,NH平分∠PNC,
∴∠JPQ=∠JPN﹣![]() ∠MPN
∠MPN
=![]() (∠ENC﹣
(∠ENC﹣![]() ∠MPN)
∠MPN)
=![]() (∠AOE﹣
(∠AOE﹣![]() ∠MPN)
∠MPN)
=![]() ∠AME
∠AME
=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1、B1、C1的坐标;
(2)将△ABC绕点C逆时针旋转90°,画出旋转后的△A2B2C2,并求出点A到A2的路径长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
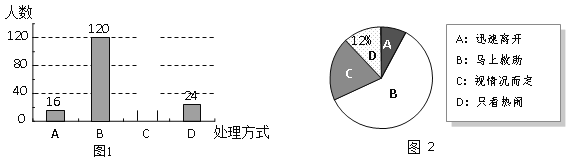
(1)该校随机抽查了 名学生?请将图1补充完整;
(2)在图2中,“视情况而定”部分所占的圆心角是 度;
(3)在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 一个游戏的中奖概率是
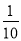 ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖B. 为了解全国中学生的心理健康情况,应该采用普查的方式
C. 一组数据6,8,7,8,8,9,10的众数和中位数都是8
D. 若甲组数据的方差
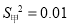 ,乙组数据的方差
,乙组数据的方差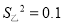 ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据6,3,4,7,6,3,5,6,求:
(1)这组数据的平均数、众数、中位数;
(2)这组数据的方差和标准差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=
 DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
相关试题

