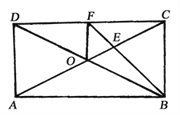
【题目】如图,已知矩形ABCD的对角线AC、BD交于O点,∠ABC的平分线交AC于E,交CD于F,∠DBF=15°,连结OF,则下列三角形①△AOD,②△COF,③△DOF,④△EOF中是等腰三角形的为________(填入序号)。
参考答案:
【答案】①②④
【解析】试题分析:根据矩形的对角线互相平分且相等,可知OA=OD=OB=OC,所以①△AOD是等腰三角形;由BF平分∠ABC,∠DBF=15°,可求得∠CFB=∠CBF=∠FBA=45°,因此可知∠ABD=30°,所以可知△BOC是等边三角形,由此可知BC=CF=OB=OC,可知②△COF为等腰三角形,由三角形的外角的性质,可知∠FEO=∠OCD+∠CFE=75°,因为CF=CO,∠FCO=30°,所以可得∠COF=75°,因此可知OF=EF,所以④△EOF是等腰三角形.
故答案为:①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长( )

A. 7 B. 8 C. 9 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】“六一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )

转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”区域的次数m
68
108
140
355
560
690
落在“铅笔”区域的频率
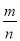
0.68
0.72
0.70
0.71
0.70
0.69
A. 当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
B. 假如你去转动转盘一次,获得铅笔的概率大约是0.70
C. 如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D. 转动转盘10次,一定有3次获得文具盒
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个数为三位数,十位数字是a,个位数字比a小2,百位数字是a的2倍,则这个三位数可表示:( )
A. 21a-2 B. 211a-2 C. 200a-2 D. 3a-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a3+a4=a7 B. (2a4)3=8a7 C. 2a3a4=2a7 D. a8÷a2=a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,要保证利润率不低于5%,该商品最多可打 ( )
A. 9折B. 8折C. 7折D. 6折
相关试题

